Advertisements
Advertisements
Question
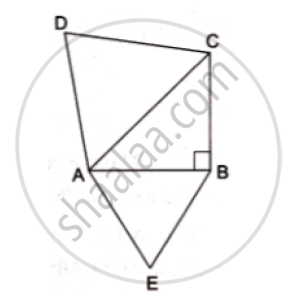
ABC is an isosceles triangle, right-angled at B. Similar triangles ACD and ABE are constructed on sides AC and AB. Find the ratio between the areas of ΔABE and ΔACD.
Solution

We have, ABC as an isosceles triangle, right angled at B.
Now, AB = BC
Applying Pythagoras theorem in right-angled triangle ABC, we get:
`AC^2=AB^2+BC^2=2AB^2 (∵ AB=AC)` .............(1)
∵ Δ ACD ∼ Δ ABE
We know that ratio of areas of 2 similar triangles is equal to squares of the ratio of their corresponding sides.
`ar(Δ ABE)/ar(ΔACD)=(AB^2)/(AC^2)=(AB^2)/(2AB^2)` [𝑓𝑟𝑜𝑚 (𝑖)]
APPEARS IN
RELATED QUESTIONS
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = x, DB = x − 2, AE = x + 2 and EC = x − 1, find the value of x.
In a ΔABC, P and Q are points on sides AB and AC respectively, such that PQ || BC. If AP = 2.4 cm, AQ = 2 cm, QC = 3 cm and BC = 6 cm, find AB and PQ.
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC.
If AD = 3.6cm, AB = 10cm and AE = 4.5cm, find EC and AC.
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC. Find the value of x, when
AD = (7x – 4) cm, AE = (5x – 2) cm, DB = (3x + 4) cm and EC = 3x cm.
In the adjoining figure, ABC is a triangle in which AB = AC. IF D and E are points on AB and AC respectively such that AD = AE, show that the points B, C, E and D are concyclic.
Find the length of altitude AD of an isosceles ΔABC in which AB = AC = 2a units and BC = a units.
Find the height of an equilateral triangle of side 12cm.
In ΔABC, AB = AC. Side BC is produced to D. Prove that `AD^2−AC^2`= BD.CD
Prove that, if a line parallel to a side of a triangle intersects the other sides in two district points, then the line divides those sides in proportion.
Construct an equilateral triangle of side 7 cm. Now, construct another triangle similar to the first triangle such that each of its sides are `5/7` times of the corresponding sides of the first triangle.
