Advertisements
Advertisements
Question
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = x, DB = x − 2, AE = x + 2 and EC = x − 1, find the value of x.
Solution
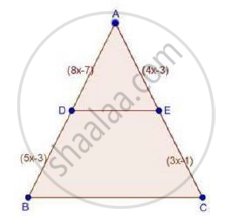
We have,
DE || BC
Therefore, by basic proportionality theorem,
We have,
`"AD"/"DB"="AE"/"EC"`
`rArrx/(x-2)=(x+2)/(x-1)`
⇒ x(x − 1) = (x + 2)(x − 2)
⇒ x2 − x = x2 − (2)2 [∵ (a – b) (a + b) = a2 − b2]
⇒ −x = −4
⇒ x = 4 cm
∴ x = 4 cm
APPEARS IN
RELATED QUESTIONS
In the given figure, PS is the bisector of ∠QPR of ΔPQR. Prove that `(QS)/(SR) = (PQ)/(PR)`

In a ΔABC, D and E are points on the sides AB and AC respectively. For the following case show that DE || BC
AB = 2cm, AD = 8cm, AE = 12 cm and AC = l8cm.
In a ΔABC, D and E are points on the sides AB and AC respectively. For the following case show that DE || BC
AB = 5.6cm, AD = 1.4cm, AC= 7.2 cm and AE = 1.8 cm.
In a ΔABC, D and E are points on the sides AB and AC respectively. For the following case show that DE || BC
AB = 10.8 cm, BD = 4.5 cm, AC = 4.8 cm and AE = 2.8 cm.
In the adjoining figure, ABC is a triangle in which AB = AC. IF D and E are points on AB and AC respectively such that AD = AE, show that the points B, C, E and D are concyclic.
An aeroplane leaves an airport and flies due north at a speed of 1000km per hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1200 km per hour. How far apart will be the two planes after` 1 1/2` hours?
Prove that, if a line parallel to a side of a triangle intersects the other sides in two district points, then the line divides those sides in proportion.
In fig., PS = 2, SQ = 6, QR = 5, PT = x and TR = y. Then find the pair of value of x and y such that ST || side QR.
O is the point of intersection of the diagonals AC and BD of a trapezium ABCD with AB || DC. Through O, a line segment PQ is drawn parallel to AB meeting AD in P and BC in Q. Prove that PO = QO.
In the given figure, Sand Tare points on sides PQ and PR, respectively of ΔPQR such that ST is parallel to QR and SQ = TR. Prove that ΔPQR is an isosceles triangles.