Advertisements
Advertisements
Question
In the given figure, PS is the bisector of ∠QPR of ΔPQR. Prove that `(QS)/(SR) = (PQ)/(PR)`

Solution
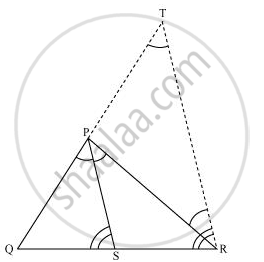
Let us draw a line segment RT parallel to SP which intersects extended line segment QP at point T.
Given that, PS is the angle bisector of ∠QPR.
∠QPS = ∠SPR … (1)
By construction,
∠SPR = ∠PRT (As PS || TR) … (2)
∠QPS = ∠QTR (As PS || TR) … (3)
Using these equations, we obtain
∠PRT = ∠QTR
∴ PT = PR
By construction,
PS || TR
By using basic proportionality theorem for ΔQTR,
`(QS)/(SR) = (QP)/(PT)`
`=>(QS)/(SR) = (PQ)/(PR) (∵ PT = PR)`
APPEARS IN
RELATED QUESTIONS
In the given figure, D is a point on side BC of ΔABC such that ∠ADC=∠BAC . Prove that AD is the bisector of ∠BAC.
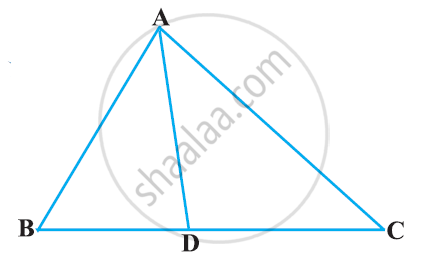
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If `"AD"/"DB"=2/3` and AC = 18 cm, find AE
In three line segments OA, OB, and OC, points L, M, N respectively are so chosen that LM || AB and MN || BC but neither of L, M, N nor of A, B, C are collinear. Show that LN ||AC.
If D and E are points on sides AB and AC respectively of a ΔABC such that DE || BC and BD = CE. Prove that ΔABC is isosceles.
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC.
If AD = 3.6cm, AB = 10cm and AE = 4.5cm, find EC and AC.
Show that the line segment which joins the midpoints of the oblique sides of a trapezium is parallel sides
Find the length of altitude AD of an isosceles ΔABC in which AB = AC = 2a units and BC = a units.
In triangle BMP and CNR it is given that PB= 5 cm, MP = 6cm BM = 9 cm and NR = 9cm. If ΔBMP∼ ΔCNR then find the perimeter of ΔCNR
In figure, PA, QB, RC and SD are all perpendiculars to a line l, AB = 6 cm, BC = 9 cm, CD = 12 cm and SP = 36 cm. Find PQ, QR and RS.
O is the point of intersection of the diagonals AC and BD of a trapezium ABCD with AB || DC. Through O, a line segment PQ is drawn parallel to AB meeting AD in P and BC in Q. Prove that PO = QO.
