Advertisements
Advertisements
Question
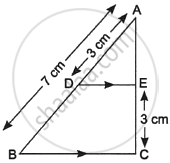
In figure, PA, QB, RC and SD are all perpendiculars to a line l, AB = 6 cm, BC = 9 cm, CD = 12 cm and SP = 36 cm. Find PQ, QR and RS.
Solution
Given, AB = 6 cm, BC = 9 cm, CD = 12 cm and SP = 36 cm
Also, PA, QB, RC and SD are all perpendiculars to line l
∴ PA || QB || RC || SD
By basic proportionality theorem,
PQ : QR : RS = AB : BC : CD
= 6 : 9 : 12
Let PQ = 6x, QR = 9x and RS = 12x
Since, length of PS = 36 cm
∴ PQ + QR + RS = 36
⇒ 6x + 9x + 12x = 36
⇒ 27x = 36
∴ x = `36/27 = 4/3`
Now, PQ = 6x
= `6 xx 4/3`
= 8 cm
QR = 9x
= `9 xx 4/3`
= 12 cm
And RS = 12x
= `12 xx 4/3`
= 16 cm
APPEARS IN
RELATED QUESTIONS
In below Fig., state if PQ || EF.
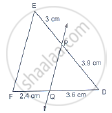
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC.
If` (AD)/(AB) = 8/15 and EC = 3.5cm`, find AE.
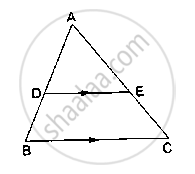
In the given figure, ABCD is a trapezium in which AB║DC and its diagonals intersect at O. If AO = (5x – 7), OC = (2x + 1) , BO = (7x – 5) and OD = (7x + 1), find the value of x.

ABCD is a parallelogram in which P is the midpoint of DC and Q is a point on AC such that CQ = `1/4` AC. If PQ produced meets BC at R, prove that R is the midpoint of BC.

ΔABC is an isosceles triangle with AB = AC = 13cm. The length of altitude from A on BC is 5cm. Find BC.
Find the length of a diagonal of a rectangle whose adjacent sides are 30cm and 16cm.
In the given figure, in ∆ABC, point D on side BC is such that, ∠BAC = ∠ADC. Prove that, CA2 = CB × CD
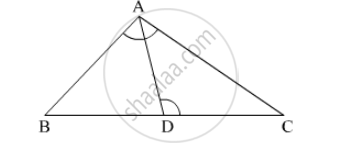
Find the value of x for which DE || AB in figure.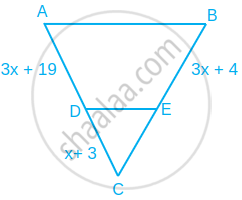
Construct an equilateral triangle of side 7 cm. Now, construct another triangle similar to the first triangle such that each of its sides are `5/7` times of the corresponding sides of the first triangle.
In the given figure, DE || BC. If AD = 3 cm, AB = 7 cm and EC = 3 cm, then the length of AE is ______.