Advertisements
Advertisements
Question
ΔABC is an isosceles triangle with AB = AC = 13cm. The length of altitude from A on BC is 5cm. Find BC.
Solution
It is given that Δ ABC is an isosceles triangle.
Also, AB = AC = 13 cm
Suppose the altitude from A on BC meets BC at D. Therefore, D is the midpoint of BC.
AD =5 cm
Δ 𝐴𝐷𝐵 𝑎𝑛𝑑 Δ 𝐴𝐷𝐶 are right-angled triangles.
Applying Pythagoras theorem, we have;
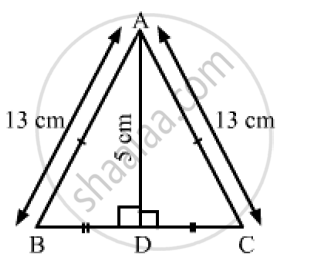
`AB^2=AD^2+BD^2`
`BD^2=AB^2-AD^2=13^2-5^2`
`BD^2=169-25=144`
`BD=sqrt144=12`
Hence,
`BC=2(BD)=2xx12=24 cm`
APPEARS IN
RELATED QUESTIONS
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If `"AD"/"BD"=4/5` and EC = 2.5 cm, find AE
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 4x − 3, AE = 8x – 7, BD = 3x – 1 and CE = 5x − 3, find the volume of x.
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 2.5 cm, BD = 3.0 cm and AE = 3.75 cm, find the length of AC.
In below Fig., state if PQ || EF.
State the midpoint theorem
From fig., seg PQ || side BC, AP = x + 3, PB = x – 3, AQ = x + 5, QC = x – 2, then complete the activity to find the value of x.
In ΔPQB, PQ || side BC
`"AP"/"PB" = "AQ"/(["______"])` ...[______]
`(x + 3)/(x - 3) = (x + 5)/(["______"])`
(x + 3) [______] = (x + 5)(x – 3)
x2 + x – [______] = x2 + 2x – 15
x = [______]
In ΔABC, AB = 6 cm and DE || BC such that AE = `1/4` AC then the length of AD is ______.
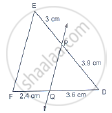
Find the value of x for which DE || AB in figure.
In figure, line segment DF intersect the side AC of a triangle ABC at the point E such that E is the mid-point of CA and ∠AEF = ∠AFE. Prove that `(BD)/(CD) = (BF)/(CE)`.
In the given figure, PQ || AC. If BP = 4 cm, AP = 2.4 cm and BQ = 5 cm, then length of BC is ______.

