Advertisements
Advertisements
Question
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 4x − 3, AE = 8x – 7, BD = 3x – 1 and CE = 5x − 3, find the volume of x.
Solution
We have, DE || BC
Therefore, by basic proportionality theorem,
We have,
`"AD"/"DB"="AE"/"EC"`
`rArr(4x-3)/(3x-1)=(8x-7)/(5x-3)`
⇒ (4x − 3)(5x − 3) = (8x − 7)(3x − 1)
⇒ 4x(5x − 3) − 3(5x − 3) = 8x(3x − 1) − 7(3x − 1)
⇒ 20x2 − 12x − 15x + 9 = 24x2 − 8x − 21x + 7
⇒ 4x2 − 2x − 2 = 0
⇒ 2(2x2 − x − 1)= 0
⇒ 2x2 − x − 1 = 0
⇒ 2x2 − 2x + 1x − 1 = 0
⇒ 2x(x − 1) + 1(x − 1) = 0
⇒ (2x + 1) (x – 1) = 0
⇒ 2x + 1 = 0 or x – 1 = 0
⇒ x = −1/2 or x = 1
x = −1/2 is not possible
∴ x = 1
APPEARS IN
RELATED QUESTIONS
In the following figure, DE || AC and DF || AE. Prove that `("BF")/("FE") = ("BE")/("EC")`

In the given figure, D is a point on side BC of ΔABC such that ∠ADC=∠BAC . Prove that AD is the bisector of ∠BAC.
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 4, AE = 8, DB = x – 4, and EC = 3x – 19, find x.
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 8x − 7, DB = 5x − 3, AE = 4x − 3 and EC = (3x − 1), find the value of x.
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC.
If `(AD)/(DB) = 4/7` and AC = 6.6cm, find AE.
In the given figure, in ∆ABC, point D on side BC is such that, ∠BAC = ∠ADC. Prove that, CA2 = CB × CD
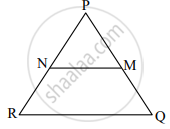
In ΔPQR, NM || RQ. If PM = 15, MQ = 10, NR = 8, then find PN.
In fig., line BC || line DE, AB = 2, BD = 3, AC = 4 and CE = x, then find the value of x
From fig., seg PQ || side BC, AP = x + 3, PB = x – 3, AQ = x + 5, QC = x – 2, then complete the activity to find the value of x.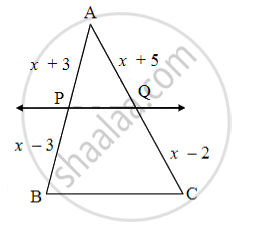
In ΔPQB, PQ || side BC
`"AP"/"PB" = "AQ"/(["______"])` ...[______]
`(x + 3)/(x - 3) = (x + 5)/(["______"])`
(x + 3) [______] = (x + 5)(x – 3)
x2 + x – [______] = x2 + 2x – 15
x = [______]
State and prove Basic Proportionality theorem.
