Advertisements
Advertisements
Question
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 8x − 7, DB = 5x − 3, AE = 4x − 3 and EC = (3x − 1), find the value of x.
Solution
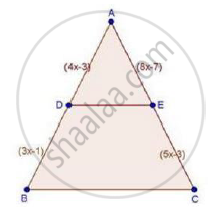
We have,
DE || BC
Therefore, by basic proportionality theorem, we have,
`"AD"/"DB"="AE"/"EC"`
`rArr(8x-7)/(5x-3)=(4x-3)/(3x-1)`
⇒ (8x − 7)(3x − 1) = (4x − 3)(5x − 3)
⇒ 24x2 − 8x − 21x + 7 = 20x2 − 12x − 15x + 9
⇒ 24x2 − 20x2 − 29x + 27x + 7 − 9 = 0
⇒ 4x2 − 2x − 2 = 0
⇒ 2[2x2 − x − 1] = 0
⇒ 2x2 − x − 1 = 0
⇒ 2x2 − 2x + 1x − 1 = 0
⇒ 2x(x − 1) + 1(x − 1) = 0
⇒ (2x + 1) (x – 1) = 0
⇒ 2x + 1 = 0 or x – 1 = 0
⇒ x = −1/2 or x = 1
𝑥 = −1/2 is not possible
∴ x = 1
RELATED QUESTIONS
In the given figure, PS is the bisector of ∠QPR of ΔPQR. Prove that `(QS)/(SR) = (PQ)/(PR)`

In the given figure, D is a point on side BC of ΔABC such that ∠ADC=∠BAC . Prove that AD is the bisector of ∠BAC.
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 4, AE = 8, DB = x – 4, and EC = 3x – 19, find x.
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 8cm, AB = 12 cm and AE = 12 cm, find CE.
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = x, DB = x − 2, AE = x + 2 and EC = x − 1, find the value of x.
In a ΔABC, D and E are points on the sides AB and AC respectively. For the following case show that DE || BC
AB = 10.8 cm, BD = 4.5 cm, AC = 4.8 cm and AE = 2.8 cm.
In a ΔABC, D and E are points on AB and AC respectively such that DE || BC. If AD = 2.4cm, AE = 3.2 cm, DE = 2cm and BC = 5 cm, find BD and CE.
M and N are points on the sides PQ and PR respectively of a ΔPQR. For the following case, state whether MN || QR
PM = 4cm, QM = 4.5 cm, PN = 4 cm and NR = 4.5 cm
ΔABC and ΔDBC lie on the same side of BC, as shown in the figure. From a point P on BC, PQ||AB and PR||BD are drawn, meeting AC at Q and CD at R respectively. Prove that QR||AD.
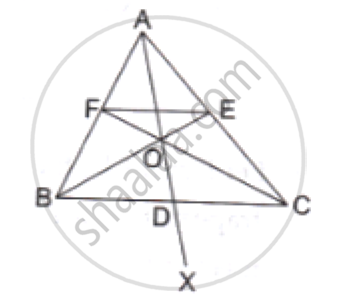
In the given figure, side BC of a ΔABC is bisected at D
and O is any point on AD. BO and CO produced meet
AC and AB at E and F respectively, and AD is
produced to X so that D is the midpoint of OX.
Prove that AO : AX = AF : AB and show that EF║BC.
ΔABC is am equilateral triangle of side 2a units. Find each of its altitudes.
In the given figure, ∠ACB 90° CD ⊥ AB Prove that `(BC^2)/(AC^2)=(BD)/(AD)`

◻ABCD is a parallelogram point E is on side BC. Line DE intersects ray AB in point T. Prove that DE × BE = CE × TE.

In ΔPQR, NM || RQ. If PM = 15, MQ = 10, NR = 8, then find PN.
From fig., seg PQ || side BC, AP = x + 3, PB = x – 3, AQ = x + 5, QC = x – 2, then complete the activity to find the value of x.
In ΔPQB, PQ || side BC
`"AP"/"PB" = "AQ"/(["______"])` ...[______]
`(x + 3)/(x - 3) = (x + 5)/(["______"])`
(x + 3) [______] = (x + 5)(x – 3)
x2 + x – [______] = x2 + 2x – 15
x = [______]
In fig., PS = 2, SQ = 6, QR = 5, PT = x and TR = y. Then find the pair of value of x and y such that ST || side QR.
ΔABC ~ ΔDEF. If AB = 4 cm, BC = 3.5 cm, CA = 2.5 cm and DF = 7.5 cm, then the perimeter of ΔDEF is ______.
In figure, PA, QB, RC and SD are all perpendiculars to a line l, AB = 6 cm, BC = 9 cm, CD = 12 cm and SP = 36 cm. Find PQ, QR and RS.
In figure, line segment DF intersect the side AC of a triangle ABC at the point E such that E is the mid-point of CA and ∠AEF = ∠AFE. Prove that `(BD)/(CD) = (BF)/(CE)`.
Construct an equilateral triangle of side 7 cm. Now, construct another triangle similar to the first triangle such that each of its sides are `5/7` times of the corresponding sides of the first triangle.
Prove that If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio. In the figure, find EC if `(AD)/(DB) = (AE)/(EC)` using the above theorem.

In the given figure, ABC is a triangle in which DE||BC. If AD = x, DB = x – 2, AE = x + 2 and EC = x – 1, then find the value of x.
In the given figure, PQ || AC. If BP = 4 cm, AP = 2.4 cm and BQ = 5 cm, then length of BC is ______.

In the given figure ∠CEF = ∠CFE. F is the midpoint of DC. Prove that `(AB)/(BD) = (AE)/(FD)`
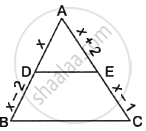
State and prove Basic Proportionality theorem.
