Advertisements
Advertisements
Question
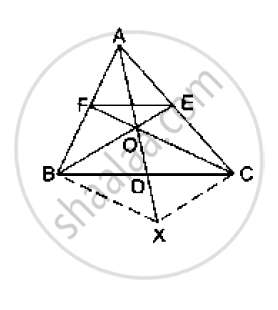
In the given figure, side BC of a ΔABC is bisected at D
and O is any point on AD. BO and CO produced meet
AC and AB at E and F respectively, and AD is
produced to X so that D is the midpoint of OX.
Prove that AO : AX = AF : AB and show that EF║BC.
Solution
It is give that BC is bisected at D.
∴ BD = DC
It is also given that OD =OX
The diagonals OX and BC of quadrilateral BOCX bisect each other.
Therefore, BOCX is a parallelogram.
∴ BO || CX and BX || CO
BX || CF and CX || BE
BX || OF and CX || OE
Applying Thales’ theorem in Δ ABX, we get:
Also, in Δ ACX, CX || OE.
Therefore by Thales’ theorem, we get:
From (1) and (2), we have:
Applying the converse of Theorem in Δ ABC, EF || CB.
This completes the proof.
APPEARS IN
RELATED QUESTIONS
In a ΔABC, P and Q are points on sides AB and AC respectively, such that PQ || BC. If AP = 2.4 cm, AQ = 2 cm, QC = 3 cm and BC = 6 cm, find AB and PQ.
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC.
If
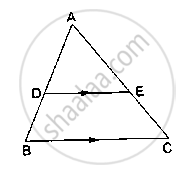
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC. Find the value of x, when
AD = (7x – 4) cm, AE = (5x – 2) cm, DB = (3x + 4) cm and EC = 3x cm.
ΔABC is am equilateral triangle of side 2a units. Find each of its altitudes.
An aeroplane leaves an airport and flies due north at a speed of 1000km per hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1200 km per hour. How far apart will be the two planes after
In a ABC , AD is a median and AL ⊥ BC .
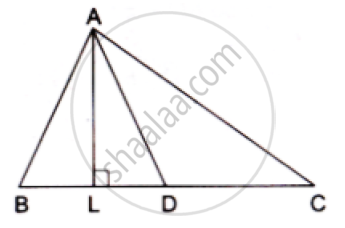
Prove that
(a)
(b)
(c)
State the basic proportionality theorem.
State and converse of Thale’s theorem.
In fig, seg DE || sec BC, identify the correct statement.

A line is parallel to one side of triangle which intersects remaining two sides in two distinct points then that line divides sides in same proportion.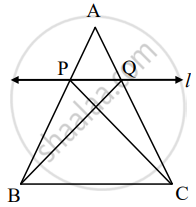
Given: In ΔABC line l || side BC and line l intersect side AB in P and side AC in Q.
To prove:
Construction: Draw CP and BQ
Proof: ΔAPQ and ΔPQB have equal height.
ΔPQC and ΔPQB have [______] is common base.
Seg PQ || Seg BC, hence height of ΔAPQ and ΔPQB.
A(ΔPQC) = A(Δ______) ......(iii)
