Advertisements
Advertisements
Question
ΔABC is am equilateral triangle of side 2a units. Find each of its altitudes.
Solution
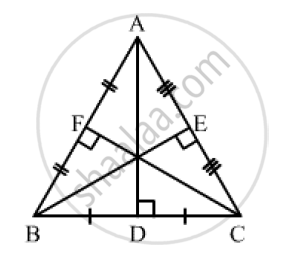
Let AD, BE and CF be the altitudes of ΔABC meeting BC, AC and AB at D, E and F, respectively.
Then, D, E and F are the midpoint of BC, AC and AB, respectively.
In right-angled ΔABD, we have:
AB = 2a and BD = a
Applying Pythagoras theorem, we get:
`AB^2=AD^2+BD^2`
`AD^2=AB^2-BD^2=(2a)^2-a^2`
`AD^2=4a^2-a^2=3a^2`
`AD=sqrt3a units`
Similarly,
`BE=asqrt3 unit and CF=a sqrt3 unitst`
APPEARS IN
RELATED QUESTIONS
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 4 cm, DB = 4.5 cm and AE = 8 cm, find AC.
In a ΔABC, D and E are points on the sides AB and AC respectively. For the following case show that DE || BC
AB = 2cm, AD = 8cm, AE = 12 cm and AC = l8cm.
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC.
If` (AD)/(AB) = 8/15 and EC = 3.5cm`, find AE.
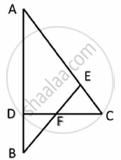
In the given figure, ∠ACB 90° CD ⊥ AB Prove that `(BC^2)/(AC^2)=(BD)/(AD)`

An aeroplane leaves an airport and flies due north at a speed of 1000km per hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1200 km per hour. How far apart will be the two planes after` 1 1/2` hours?
State the midpoint theorem
◻ABCD is a parallelogram point E is on side BC. Line DE intersects ray AB in point T. Prove that DE × BE = CE × TE.

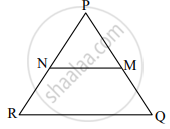
In ΔPQR, NM || RQ. If PM = 15, MQ = 10, NR = 8, then find PN.
In ΔABC, AB = 6 cm and DE || BC such that AE = `1/4` AC then the length of AD is ______.
In the given figure ∠CEF = ∠CFE. F is the midpoint of DC. Prove that `(AB)/(BD) = (AE)/(FD)`