Advertisements
Advertisements
Question
In a ΔABC, D and E are points on the sides AB and AC respectively. For the following case show that DE || BC
AB = 2cm, AD = 8cm, AE = 12 cm and AC = l8cm.
Solution
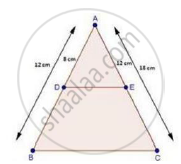
AB = 12 cm, AD = 12 cm and AC = 18 cm.
∴ DB = AB – AD
= 12 – 8
⇒ DB = 4 cm
And, EC = AC – AE
= 18 – 12
⇒ EC = 6 cm
Now, `"AD"/"DB"=8/4=2/1` [∵ DB = 4 cm]
And, `"AE"/"EC"=12/6=2/1` [∵ EC = 6 cm]
`rArr"AD"/"DB"="AE"/"EC"`
Thus, DE divides sides AB and AC of ΔABC in the same ratio.
Therefore, by the converse of basic proportionality theorem,
We have, DE || BC
APPEARS IN
RELATED QUESTIONS
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If `"AD"/"BD"=4/5` and EC = 2.5 cm, find AE
In a ΔABC, D and E are points on the sides AB and AC respectively. For the following case show that DE || BC
AB = 10.8 cm, BD = 4.5 cm, AC = 4.8 cm and AE = 2.8 cm.
M and N are points on the sides PQ and PR respectively of a ΔPQR. For the following case, state whether MN || QR
PM = 4cm, QM = 4.5 cm, PN = 4 cm and NR = 4.5 cm
If D and E are points on sides AB and AC respectively of a ΔABC such that DE || BC and BD = CE. Prove that ΔABC is isosceles.
D and E are the points on the sides AB and AC respectively of a ΔABC such that: AD = 8 cm, DB = 12 cm, AE = 6 cm and CE = 9 cm. Prove that BC = 5/2 DE.
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC.
If` (AD)/(AB) = 8/15 and EC = 3.5cm`, find AE.
Show that the line segment which joins the midpoints of the oblique sides of a trapezium is parallel sides
ΔABC is am equilateral triangle of side 2a units. Find each of its altitudes.
Find the length of a diagonal of a rectangle whose adjacent sides are 30cm and 16cm.
In ΔABC, D is the midpoint of BC and AE⊥BC. If AC>AB, show that `AB^2= AD^2+1/4 BC^2 −BC.DE `
