Advertisements
Advertisements
Question
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 2.5 cm, BD = 3.0 cm and AE = 3.75 cm, find the length of AC.
Solution
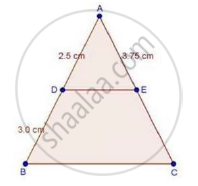
We have, DE || BC
Therefore, by basic proportionality theorem, we have,
`"AD"/"DB"="AE"/"EC"`
`rArr2.5/3.0=3.75/"EC"`
`rArr"EC"=(3.75xx3)/2.5=(375xx3)/250`
`rArr"EC"=(15xx3)/10=45/10=4.5` cm
Now, AC = AE + EC = 3.75 + 4.5 = 8.25
∴ AC = 8.25 cm
APPEARS IN
RELATED QUESTIONS
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 4 cm, DB = 4.5 cm and AE = 8 cm, find AC.
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 2 cm, AB = 6 cm and AC = 9 cm, find AE.
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 8x − 7, DB = 5x − 3, AE = 4x − 3 and EC = (3x − 1), find the value of x.
In a ΔABC, D and E are points on the sides AB and AC respectively. For the following case show that DE || BC
AD = 5.7 cm, BD = 9.5 cm, AE = 3.3 cm and EC = 5.5 cm.
Show that the line segment which joins the midpoints of the oblique sides of a trapezium is parallel sides
In the given figure, ∠ACB 90° CD ⊥ AB Prove that `(BC^2)/(AC^2)=(BD)/(AD)`

State the midpoint theorem
◻ABCD is a parallelogram point E is on side BC. Line DE intersects ray AB in point T. Prove that DE × BE = CE × TE.

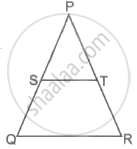
In the given figure, Sand Tare points on sides PQ and PR, respectively of ΔPQR such that ST is parallel to QR and SQ = TR. Prove that ΔPQR is an isosceles triangles.
In the given figure ∠CEF = ∠CFE. F is the midpoint of DC. Prove that `(AB)/(BD) = (AE)/(FD)`