Advertisements
Advertisements
Question
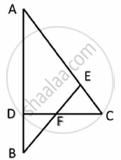
In a ΔABC, D and E are points on the sides AB and AC respectively. For the following case show that DE || BC
AD = 5.7 cm, BD = 9.5 cm, AE = 3.3 cm and EC = 5.5 cm.
Solution
We have,
DE || BC
We have, AD = 5.7 cm, BD = 9.5 cm, AE = 3.3 cm and EC = 5.5 cm
Now, `"AD"/"DB"=5.7/9.5=57/95`
`rArr"AD"/"DB"=3/5`
And, `"AE"/"EC"=3.3/5.5=33/55`
`rArr"AE"/"EC"=3/5`
Thus DE divides sides AB and AC of ΔABC in the same ratio.
Therefore, by the converse of basic proportionality theorem.
We have DE || BC
APPEARS IN
RELATED QUESTIONS
In a ΔABC, D and E are points on the sides AB and AC respectively. For the following case show that DE || BC
AB = 2cm, AD = 8cm, AE = 12 cm and AC = l8cm.
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC. Find the value of x, when
AD = x cm, DB = (x – 2) cm, AE = (x + 2) cm and EC = (x – 1) cm.
ABCD is a parallelogram in which P is the midpoint of DC and Q is a point on AC such that CQ = `1/4` AC. If PQ produced meets BC at R, prove that R is the midpoint of BC.

Each of the equal sides of an isosceles triangle is 25 cm. Find the length of its altitude if the base is 14 cm.
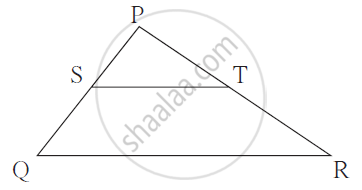
In Δ PQR, points S and T
are the midpoints of sides PQ
and PR respectively.
If ST = 6.2 then find the length of QR.
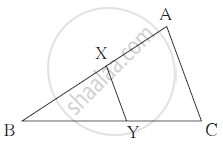
In the adjoining figure,
seg XY || seg AC, If 3AX = 2BX
and XY = 9 then find the length of AC.
In fig., PS = 2, SQ = 6, QR = 5, PT = x and TR = y. Then find the pair of value of x and y such that ST || side QR.
Find the value of x for which DE || AB in figure.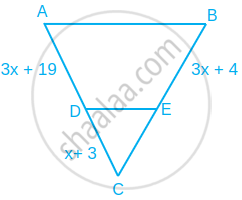
Prove that If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio. In the figure, find EC if `(AD)/(DB) = (AE)/(EC)` using the above theorem.

In the given figure ∠CEF = ∠CFE. F is the midpoint of DC. Prove that `(AB)/(BD) = (AE)/(FD)`