Advertisements
Advertisements
Question
ABCD is a parallelogram in which P is the midpoint of DC and Q is a point on AC such that CQ = `1/4` AC. If PQ produced meets BC at R, prove that R is the midpoint of BC.

Solution
We know that the diagonals of a parallelogram bisect each other.
Therefore,
`CS=1/2AC` ................(1)
Also, it is given that` CQ=1/4 AC ` .............(2)
Dividing equation (ii) by (i), we get:
`CQ/CS=((1/4)AC)/((1/2)AC)`
Or, CQ=`1/2`CS
Hence, Q is the midpoint of CS.
Therefore, according to midpoint theorem in ΔCSD
PQ || DS
If PQ || DS, we can say that QR || SB
In Δ CSB, Q is midpoint of CS and QR ‖ SB.
Applying converse of midpoint theorem , we conclude that R is the midpoint of CB.
This completes the proof.
APPEARS IN
RELATED QUESTIONS
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 4x − 3, AE = 8x – 7, BD = 3x – 1 and CE = 5x − 3, find the volume of x.
In a ΔABC, D and E are points on the sides AB and AC respectively. For the following case show that DE || BC
AB = 5.6cm, AD = 1.4cm, AC= 7.2 cm and AE = 1.8 cm.
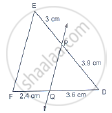
In below Fig., state if PQ || EF.
Show that the line segment which joins the midpoints of the oblique sides of a trapezium is parallel sides
Two vertical poles of height 9m and 14m stand on a plane ground. If the distance between their feet is 12m, find the distance between their tops.
Find the length of altitude AD of an isosceles ΔABC in which AB = AC = 2a units and BC = a units.
In ΔABC, AB = AC. Side BC is produced to D. Prove that `AD^2−AC^2`= BD.CD
In triangle BMP and CNR it is given that PB= 5 cm, MP = 6cm BM = 9 cm and NR = 9cm. If ΔBMP∼ ΔCNR then find the perimeter of ΔCNR
In figure, PA, QB, RC and SD are all perpendiculars to a line l, AB = 6 cm, BC = 9 cm, CD = 12 cm and SP = 36 cm. Find PQ, QR and RS.
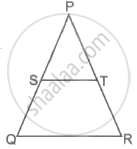
In the given figure, Sand Tare points on sides PQ and PR, respectively of ΔPQR such that ST is parallel to QR and SQ = TR. Prove that ΔPQR is an isosceles triangles.