Advertisements
Advertisements
प्रश्न
ABCD is a parallelogram in which P is the midpoint of DC and Q is a point on AC such that CQ = `1/4` AC. If PQ produced meets BC at R, prove that R is the midpoint of BC.

उत्तर
We know that the diagonals of a parallelogram bisect each other.
Therefore,
`CS=1/2AC` ................(1)
Also, it is given that` CQ=1/4 AC ` .............(2)
Dividing equation (ii) by (i), we get:
`CQ/CS=((1/4)AC)/((1/2)AC)`
Or, CQ=`1/2`CS
Hence, Q is the midpoint of CS.
Therefore, according to midpoint theorem in ΔCSD
PQ || DS
If PQ || DS, we can say that QR || SB
In Δ CSB, Q is midpoint of CS and QR ‖ SB.
Applying converse of midpoint theorem , we conclude that R is the midpoint of CB.
This completes the proof.
APPEARS IN
संबंधित प्रश्न
In the given figure, PS is the bisector of ∠QPR of ΔPQR. Prove that `(QS)/(SR) = (PQ)/(PR)`

In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 4x − 3, AE = 8x – 7, BD = 3x – 1 and CE = 5x − 3, find the volume of x.
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC.
If AD = 3.6cm, AB = 10cm and AE = 4.5cm, find EC and AC.
In the given figure, ABCD is a trapezium in which AB║DC and its diagonals intersect at O. If AO = (5x – 7), OC = (2x + 1) , BO = (7x – 5) and OD = (7x + 1), find the value of x.

Find the height of an equilateral triangle of side 12cm.
Find the length of each side of a rhombus whose diagonals are 24cm and 10cm long.
In a ABC , AD is a median and AL ⊥ BC .
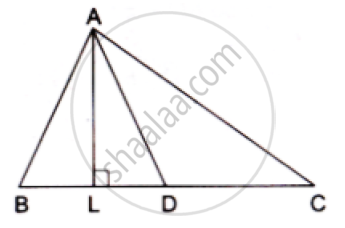
Prove that
(a) `AC^2=AD^2+BC DL+((BC)/2)^2`
(b) `AB^2=AD^2-BC DL+((BC)/2)^2`
(c) `AC^2+AB^2=2.AD^2+1/2BC^2`
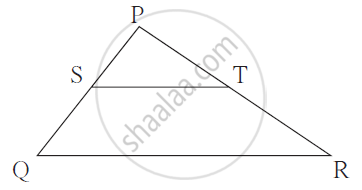
In Δ PQR, points S and T
are the midpoints of sides PQ
and PR respectively.
If ST = 6.2 then find the length of QR.
Draw an isosceles triangle with base 5 cm and height 4 cm. Draw a triangle similar to the triangle drawn whose sides are `2/3` times the sides of the triangle.
Prove that, if a line parallel to a side of a triangle intersects the other sides in two district points, then the line divides those sides in proportion.
