Advertisements
Advertisements
प्रश्न
In the given figure, ABCD is a trapezium in which AB║DC and its diagonals intersect at O. If AO = (5x – 7), OC = (2x + 1) , BO = (7x – 5) and OD = (7x + 1), find the value of x.

उत्तर
In trapezium ABCD, AB ‖ CD and the diagonals AC and BD intersect at O. Therefore,
`(AO)/(OC)=(BO)/(OD)`
⇒ `(5x-7)/(2x+1)=(7x-5)/(7x+1)`
⟹ (5x-7) (7x+1) = (7x-5) (2x+1)
⟹`35x^2+5x-49x-7=14x^2-10x+7x-5`
⟹ `21x^2-41x-2=0`
⟹`21x^2-42x+x-2=0`
⟹`21x(x-2)+1(x-2)=0`
⟹`(x-2) (2x+1)=0`
⟹ `x=2,1/21`
∵ `x ≠-1/21`
∴ x=2
APPEARS IN
संबंधित प्रश्न
In the given figure, D is a point on side BC of ΔABC such that ∠ADC=∠BAC . Prove that AD is the bisector of ∠BAC.
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 4x − 3, AE = 8x – 7, BD = 3x – 1 and CE = 5x − 3, find the volume of x.
If D and E are points on sides AB and AC respectively of a ΔABC such that DE || BC and BD = CE. Prove that ΔABC is isosceles.
Find the height of an equilateral triangle of side 12cm.
State the basic proportionality theorem.
State and converse of Thale’s theorem.
Prove that, if a line parallel to a side of a triangle intersects the other sides in two district points, then the line divides those sides in proportion.
In the given figure ΔABC ~ ΔPQR, PM is median of ΔPQR. If ar ΔABC = 289 cm², BC = 17 cm, MR = 6.5 cm then the area of ΔPQM is ______.
 |
 |
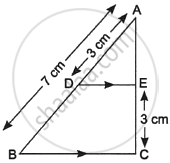
In figure, PA, QB, RC and SD are all perpendiculars to a line l, AB = 6 cm, BC = 9 cm, CD = 12 cm and SP = 36 cm. Find PQ, QR and RS.
In the given figure, DE || BC. If AD = 3 cm, AB = 7 cm and EC = 3 cm, then the length of AE is ______.