Advertisements
Advertisements
प्रश्न
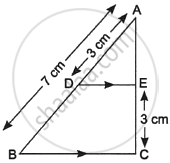
In the given figure, DE || BC. If AD = 3 cm, AB = 7 cm and EC = 3 cm, then the length of AE is ______.
पर्याय
2 cm
2.25 cm
3.5 cm
4 cm
उत्तर
In the given figure, DE || BC. If AD = 3 cm, AB = 7 cm and EC = 3 cm, then the length of AE is 2.25 cm.

Explanation:
Given, AD = 3 cm, AB = 7 cm, EC = 3 cm.
Let AE = x cm
∴ AC = AE + EC = x + 3 cm
As we know that
`(AD)/(AB) = (AE)/(AC)`
`\implies 3/7 = x/(x + 3)`
`\implies` 3(x + 3) = 7x
`\implies` 3x + 9 = 7x
`\implies` 7x – 3x = 9
`\implies` 4x = 9
`\implies` x = `9/4` = 2.25 cm
∴ length of AE = 2.25 cm
APPEARS IN
संबंधित प्रश्न
In a ΔABC, D and E are points on AB and AC respectively such that DE || BC. If AD = 2.4cm, AE = 3.2 cm, DE = 2cm and BC = 5 cm, find BD and CE.
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC.
If AB = 13.3cm, AC = 11.9cm and EC = 5.1cm, find AD.
In the given figure, ABCD is a trapezium in which AB║DC and its diagonals intersect at O. If AO = (5x – 7), OC = (2x + 1) , BO = (7x – 5) and OD = (7x + 1), find the value of x.

In the adjoining figure, ABC is a triangle in which AB = AC. IF D and E are points on AB and AC respectively such that AD = AE, show that the points B, C, E and D are concyclic.
Find the length of altitude AD of an isosceles ΔABC in which AB = AC = 2a units and BC = a units.
In the given figure, ∠ACB 90° CD ⊥ AB Prove that `(BC^2)/(AC^2)=(BD)/(AD)`

In ΔABC, AB = AC. Side BC is produced to D. Prove that `AD^2−AC^2`= BD.CD
ABC is an isosceles triangle, right-angled at B. Similar triangles ACD and ABE are constructed on sides AC and AB. Find the ratio between the areas of ΔABE and ΔACD.
Prove that, if a line parallel to a side of a triangle intersects the other sides in two district points, then the line divides those sides in proportion.
State and prove Basic Proportionality theorem.
