Advertisements
Advertisements
प्रश्न
In the given figure, ∠ACB 90° CD ⊥ AB Prove that `(BC^2)/(AC^2)=(BD)/(AD)`

उत्तर
Given: ∠𝐴𝐶𝐵 = 90° 𝑎𝑛𝑑 𝐶𝐷 ⊥ 𝐴𝐵
To Prove:` (BC^2)/(AC^2)=(BD)/(AD)`
Proof: In Δ ACB and Δ CDB
∠𝐴𝐶𝐵 = ∠𝐶𝐷𝐵 = 90° (𝐺𝑖𝑣𝑒𝑛)
∠𝐴𝐵𝐶 = ∠𝐶𝐵𝐷 (𝐶𝑜𝑚𝑚𝑜𝑛)
By AA similarity-criterion Δ ACB ~ ΔCDB
When two triangles are similar, then the ratios of the lengths of their corresponding sides are proportional.
`∴ (BC)/(BD)=(AB)/(BC)`
`⇒ BC^2=BD.AB` ..............(1)
In Δ ACB and Δ ADC
∠𝐴𝐶𝐵 = ∠𝐴𝐷𝐶 = 90° (𝐺𝑖𝑣𝑒𝑛)
∠𝐶𝐴𝐵 = ∠𝐷𝐴𝐶 (𝐶𝑜𝑚𝑚𝑜𝑛)
By AA similarity-criterion Δ ACB ~ ΔADC
When two triangles are similar, then the ratios of their corresponding sides are proportional.
∴ `(AC)/(AD)=(AB)/(AC)`
⇒` AC^2=AD.AB` .................(2)
Dividing (2) by (1), we get
`(BC^2)/(AC^2)=(BD)/(AD)`
APPEARS IN
संबंधित प्रश्न
M and N are points on the sides PQ and PR respectively of a ΔPQR. For the following case, state whether MN || QR
PM = 4cm, QM = 4.5 cm, PN = 4 cm and NR = 4.5 cm
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC.
If AD = 3.6cm, AB = 10cm and AE = 4.5cm, find EC and AC.
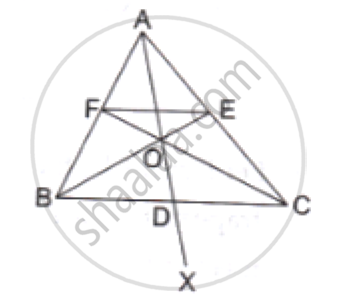
ΔABC and ΔDBC lie on the same side of BC, as shown in the figure. From a point P on BC, PQ||AB and PR||BD are drawn, meeting AC at Q and CD at R respectively. Prove that QR||AD.
A guy wire attached to a vertical pole of height 18 m is 24m long and has a stake attached to the other end. How far from the base of the pole should the stake be driven so that the wire will be taut?
ΔABC is am equilateral triangle of side 2a units. Find each of its altitudes.
Find the length of a diagonal of a rectangle whose adjacent sides are 30cm and 16cm.
In the given figure, D is the midpoint of side BC and AE⊥BC. If BC = a, AC = b, AB = c, AD = p and AE = h, prove that
(i)`B^2=p^2+ax+a^2/x`
(ii)` c^2=p^2-ax+a^2/x`
(iii) `b^2+c^2=2p^2+a^2/2`
(iv)`b^2-c^2=2ax`

ABC is an isosceles triangle, right-angled at B. Similar triangles ACD and ABE are constructed on sides AC and AB. Find the ratio between the areas of ΔABE and ΔACD.
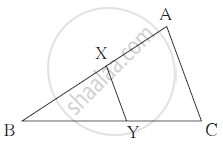
In the adjoining figure,
seg XY || seg AC, If 3AX = 2BX
and XY = 9 then find the length of AC.
O is the point of intersection of the diagonals AC and BD of a trapezium ABCD with AB || DC. Through O, a line segment PQ is drawn parallel to AB meeting AD in P and BC in Q. Prove that PO = QO.
