Advertisements
Advertisements
प्रश्न
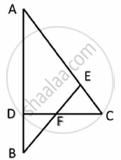
In ΔABC, D is the midpoint of BC and AE⊥BC. If AC>AB, show that `AB^2= AD^2+1/4 BC^2 −BC.DE `
उत्तर
In right-angled triangle AED, applying Pythagoras theorem, we have:
`AB^2=AE^2+ED^2` ...........(1)
In right-angled triangle AED, applying Pythagoras theorem, we have:
`AD^2=AE^2+ED^2`
`⇒ AE^2=AD^2-ED^2` ...............(2)
Therefore,
`AB^2=AD^2-ED^2+EB^2` (from(1) and (2))
`AB^2=AD^2-ED^2+(BD-DE)^2`
`=AD^2-ED^2+(1/2BC-DE)^2`
`=AD^2-DE^2+1/4BC^2+DE^2-BC.DE`
`=AD^2+1/4BC^2-BC.DE`
This completes the proof.
APPEARS IN
संबंधित प्रश्न
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = x, DB = x − 2, AE = x + 2 and EC = x − 1, find the value of x.
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 2.5 cm, BD = 3.0 cm and AE = 3.75 cm, find the length of AC.
If D and E are points on sides AB and AC respectively of a ΔABC such that DE || BC and BD = CE. Prove that ΔABC is isosceles.
In the adjoining figure, ABC is a triangle in which AB = AC. IF D and E are points on AB and AC respectively such that AD = AE, show that the points B, C, E and D are concyclic.
Two vertical poles of height 9m and 14m stand on a plane ground. If the distance between their feet is 12m, find the distance between their tops.
State the midpoint theorem
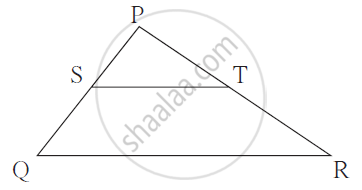
In Δ PQR, points S and T
are the midpoints of sides PQ
and PR respectively.
If ST = 6.2 then find the length of QR.
From fig., seg PQ || side BC, AP = x + 3, PB = x – 3, AQ = x + 5, QC = x – 2, then complete the activity to find the value of x.
In ΔPQB, PQ || side BC
`"AP"/"PB" = "AQ"/(["______"])` ...[______]
`(x + 3)/(x - 3) = (x + 5)/(["______"])`
(x + 3) [______] = (x + 5)(x – 3)
x2 + x – [______] = x2 + 2x – 15
x = [______]
Prove that If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio. In the figure, find EC if `(AD)/(DB) = (AE)/(EC)` using the above theorem.

In the given figure ∠CEF = ∠CFE. F is the midpoint of DC. Prove that `(AB)/(BD) = (AE)/(FD)`