Advertisements
Advertisements
प्रश्न
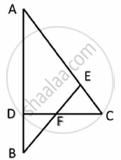
In the adjoining figure, ABC is a triangle in which AB = AC. IF D and E are points on AB and AC respectively such that AD = AE, show that the points B, C, E and D are concyclic.
उत्तर
Given:
AD = AE …(1)
AB = AC …(2)
Subtracting AD from both sides, we get:
⟹ AB – AD = AC – AD
⟹ AB – AD = AC - AE (Since, AD = AE)
⟹ BD = EC …(3)
Dividing equation (1) by equation (3), we get:
`(AD)/(DB)=(AE)/(EC)`
Applying the converse of Thales’ theorem, DE‖BC
⟹ ∠DEC + ∠ECB = 180° (Sum of interior angles on the same side of a
Transversal Line is 0°)
⟹ ∠DEC + ∠CBD = 180° (Since, AB = AC ⟹ ∠B = ∠C)
Hence, quadrilateral BCED is cyclic.
Therefore, B,C,E and D are concylic points.
APPEARS IN
संबंधित प्रश्न
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If `"AD"/"DB"=2/3` and AC = 18 cm, find AE
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 4 cm, DB = 4.5 cm and AE = 8 cm, find AC.
In a ΔABC, D and E are points on the sides AB and AC respectively. For the following case show that DE || BC
AB = 10.8 cm, BD = 4.5 cm, AC = 4.8 cm and AE = 2.8 cm.
In a ΔABC, D and E are points on AB and AC respectively such that DE || BC. If AD = 2.4cm, AE = 3.2 cm, DE = 2cm and BC = 5 cm, find BD and CE.
In below Fig., state if PQ || EF.
ΔABC is an isosceles triangle with AB = AC = 13cm. The length of altitude from A on BC is 5cm. Find BC.
A and B are respectively the points on the sides PQ and PR of a triangle PQR such that PQ = 12.5 cm, PA = 5 cm, BR = 6 cm and PB = 4 cm. Is AB || QR? Give reasons for your answer.
In figure, line segment DF intersect the side AC of a triangle ABC at the point E such that E is the mid-point of CA and ∠AEF = ∠AFE. Prove that `(BD)/(CD) = (BF)/(CE)`.
In the given figure, DE || BC. If AD = 3 cm, AB = 7 cm and EC = 3 cm, then the length of AE is ______.
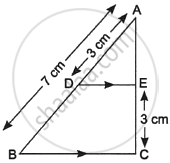
In the given figure ∠CEF = ∠CFE. F is the midpoint of DC. Prove that `(AB)/(BD) = (AE)/(FD)`