Advertisements
Advertisements
प्रश्न
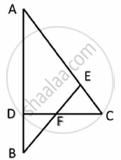
In figure, line segment DF intersect the side AC of a triangle ABC at the point E such that E is the mid-point of CA and ∠AEF = ∠AFE. Prove that `(BD)/(CD) = (BF)/(CE)`.
उत्तर
Given ΔABC, E is the mid-point of CA and ∠AEF = ∠AFE
To prove: `("BD")/("CD") = ("BF")/("CE")`
Construction: Take a point G on AB such that CG || EF
Proof: Since, E is the mid-point of CA
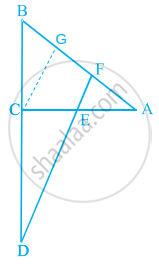
∴ CE = AE ...(i)
In ΔACG,
CG || EF and E is mid-point of CA
So, CE = GF ...(ii) [By mid-point theorem]
Now, In ΔBCG and ΔBDF,
CG || EF
∴ `("BC")/("CD") = ("BG")/("GF")` ...[By basic proportionality theorem]
⇒ `("BC")/("CD") = ("BF" - "GF")/("GF")`
⇒ `("BC")/("CD") = ("BF")/("GF") - 1`
⇒ `("BC")/("CD") + 1 = ("BF")/("CE")` ...[From equation (ii)]
⇒ `("BC" + "CD")/("CD") = ("BF")/("CE")`
⇒ `("BD")/("CD") = ("BF")/("CE")`
Hence proved.
APPEARS IN
संबंधित प्रश्न
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 4x − 3, AE = 8x – 7, BD = 3x – 1 and CE = 5x − 3, find the volume of x.
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC.
If AD = 3.6cm, AB = 10cm and AE = 4.5cm, find EC and AC.
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC. Find the value of x, when
AD = 4cm, DB = (x – 4) cm, AE = 8cm and EC = (3x – 19) cm.
A guy wire attached to a vertical pole of height 18 m is 24m long and has a stake attached to the other end. How far from the base of the pole should the stake be driven so that the wire will be taut?
ΔABC is am equilateral triangle of side 2a units. Find each of its altitudes.
State the midpoint theorem
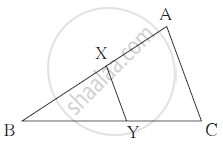
In the adjoining figure,
seg XY || seg AC, If 3AX = 2BX
and XY = 9 then find the length of AC.
In fig., PS = 2, SQ = 6, QR = 5, PT = x and TR = y. Then find the pair of value of x and y such that ST || side QR.
ΔABC ~ ΔDEF. If AB = 4 cm, BC = 3.5 cm, CA = 2.5 cm and DF = 7.5 cm, then the perimeter of ΔDEF is ______.
In the given figure ∠CEF = ∠CFE. F is the midpoint of DC. Prove that `(AB)/(BD) = (AE)/(FD)`