Advertisements
Advertisements
प्रश्न
Prove that the area of the semicircle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the semicircles drawn on the other two sides of the triangle.
उत्तर
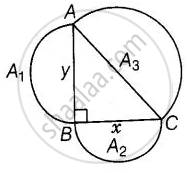
Let ABC be a right triangle, right angled at B and AB = y, BC = x.
Three semi-circles are drawn on the sides AB, BC and AC, respectively with diameters AB, BC and AC, respectively.
Again, let area of circles with diameters AB, BC and AC are respectively A1, A2 and A3.
To prove: A3 = A1 + A2
Proof: In ΔABC,
By pythagoras theorem,
AC2 = AB2 + BC2
⇒ AC2 = y2 + x2
⇒ AC = `sqrt(y^2 + x^2)`
We know that,
Area of a semi-circle with radius,
r = `(pir^2)/2`
∴ Area of semi-circle drawn on AC,
A3 = `pi/2(("AC")/2)^2`
= `pi/2(sqrt(y^2 + x^2)/2)^2`
⇒ A3 = `(pi(y^2 + x^2))/8` ...(i)
Now, area of semi-circle drawn on AB,
A1 = `pi/2 (("AB")/2)^2`
⇒ A1 = `pi/2(y/2)^2`
⇒ A1 = `(piy^2)/8` ...(ii)
And area of semi-circle drawn on BC,
A2 = `pi/2(("BC")/2)^2`
= `pi/2(x/2)^2`
⇒ A2 = `(pix^2)/8`
On adding equations (ii) and (iii), we get
A1 + A2 = `(piy^2)/8 + (pix^2)/8`
= `(pi(y^2 + x^2))/8`
= A3 ...[From equation (i)]
⇒ A1 + A2 = A3
Hence proved.
APPEARS IN
संबंधित प्रश्न
Two poles of heights 6 m and 11 m stand on a plane ground. If the distance between the feet of the poles is 12 m, find the distance between their tops.
If the sides of the triangle are in the ratio 1: `sqrt2`: 1, show that is a right-angled triangle.
Find the value of (sin2 33 + sin2 57°)
In triangle PQR, angle Q = 90°, find: PR, if PQ = 8 cm and QR = 6 cm
Find the Pythagorean triplet from among the following set of numbers.
4, 7, 8
A right triangle has hypotenuse p cm and one side q cm. If p - q = 1, find the length of third side of the triangle.
In an equilateral triangle ABC, the side BC is trisected at D. Prove that 9 AD2 = 7 AB2.
In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AB2 = AD2 - BC x CE + `(1)/(4)"BC"^2`
A man goes 18 m due east and then 24 m due north. Find the distance of his current position from the starting point?
In a right-angled triangle ABC, if angle B = 90°, BC = 3 cm and AC = 5 cm, then the length of side AB is ______.
