Advertisements
Advertisements
प्रश्न
Prove that the area of the semicircle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the semicircles drawn on the other two sides of the triangle.
उत्तर
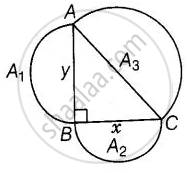
Let ABC be a right triangle, right angled at B and AB = y, BC = x.
Three semi-circles are drawn on the sides AB, BC and AC, respectively with diameters AB, BC and AC, respectively.
Again, let area of circles with diameters AB, BC and AC are respectively A1, A2 and A3.
To prove: A3 = A1 + A2
Proof: In ΔABC,
By pythagoras theorem,
AC2 = AB2 + BC2
⇒ AC2 = y2 + x2
⇒ AC = `sqrt(y^2 + x^2)`
We know that,
Area of a semi-circle with radius,
r = `(pir^2)/2`
∴ Area of semi-circle drawn on AC,
A3 = `pi/2(("AC")/2)^2`
= `pi/2(sqrt(y^2 + x^2)/2)^2`
⇒ A3 = `(pi(y^2 + x^2))/8` ...(i)
Now, area of semi-circle drawn on AB,
A1 = `pi/2 (("AB")/2)^2`
⇒ A1 = `pi/2(y/2)^2`
⇒ A1 = `(piy^2)/8` ...(ii)
And area of semi-circle drawn on BC,
A2 = `pi/2(("BC")/2)^2`
= `pi/2(x/2)^2`
⇒ A2 = `(pix^2)/8`
On adding equations (ii) and (iii), we get
A1 + A2 = `(piy^2)/8 + (pix^2)/8`
= `(pi(y^2 + x^2))/8`
= A3 ...[From equation (i)]
⇒ A1 + A2 = A3
Hence proved.
APPEARS IN
संबंधित प्रश्न
In the given figure, ∠DFE = 90°, FG ⊥ ED, If GD = 8, FG = 12, find (1) EG (2) FD and (3) EF

In triangle ABC, AB = AC = x, BC = 10 cm and the area of the triangle is 60 cm2.
Find x.
Triangle XYZ is right-angled at vertex Z. Calculate the length of YZ, if XY = 13 cm and XZ = 12 cm.
The top of a ladder of length 15 m reaches a window 9 m above the ground. What is the distance between the base of the wall and that of the ladder?
The sides of the triangle are given below. Find out which one is the right-angled triangle?
8, 15, 17
The sides of the triangle are given below. Find out which one is the right-angled triangle?
11, 12, 15
From the given figure, in ∆ABQ, if AQ = 8 cm, then AB =?

In a quadrilateral ABCD, ∠A + ∠D = 90°. Prove that AC2 + BD2 = AD2 + BC2
[Hint: Produce AB and DC to meet at E.]
Prove that the area of the equilateral triangle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the equilateral triangles drawn on the other two sides of the triangle.
In a right-angled triangle ABC, if angle B = 90°, then which of the following is true?
