Advertisements
Advertisements
प्रश्न
Triangle XYZ is right-angled at vertex Z. Calculate the length of YZ, if XY = 13 cm and XZ = 12 cm.
उत्तर
Given: ∆XYZ right angled at Z and XY = 13 cm, XZ = 12 cm.
To find: Length of YZ.
According to Pythagoras Theorem,
XY2 = XZ2 + YZ2
132 = 122 + YZ2
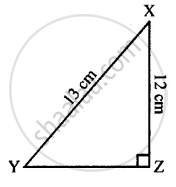
169= 144 +YZ2
169 − 144 = YZ2
25 = YZ2
∴ YZ = `sqrt25"cm"=sqrt(5xx5)` = 5 cm
APPEARS IN
संबंधित प्रश्न
In an equilateral triangle ABC, D is a point on side BC such that BD = `1/3BC` . Prove that 9 AD2 = 7 AB2
In triangle ABC, AB = AC and BD is perpendicular to AC.
Prove that: BD2 - CD2 = 2CD × AD
In a quadrilateral ABCD, ∠B = 90° and ∠D = 90°.
Prove that: 2AC2 - AB2 = BC2 + CD2 + DA2
Find the side of the square whose diagonal is `16sqrt(2)` cm.
The sides of the triangle are given below. Find out which one is the right-angled triangle?
8, 15, 17
Find the length of the hypotenuse of a triangle whose other two sides are 24cm and 7cm.
Calculate the area of a right-angled triangle whose hypotenuse is 65cm and one side is 16cm.
From a point O in the interior of aΔABC, perpendicular OD, OE and OF are drawn to the sides BC, CA and AB respectively. Prove that: AF2 + BD2 + CE2 = OA2 + OB2 + OC2 - OD2 - OE2 - OF2
Prove that the area of the semicircle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the semicircles drawn on the other two sides of the triangle.
Points A and B are on the opposite edges of a pond as shown in figure. To find the distance between the two points, the surveyor makes a right-angled triangle as shown. Find the distance AB.

