Advertisements
Advertisements
प्रश्न
In an equilateral triangle ABC, D is a point on side BC such that BD = `1/3BC` . Prove that 9 AD2 = 7 AB2
उत्तर
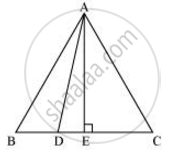
Let the side of the equilateral triangle be a, and AE be the altitude of ΔABC.
`∴ BE = EC = (BC)/2 = a/2`
And, AE = `(asqrt3)/2`
Given that, BD = `1/3BC`
∴ BD = a/3
`DE = BE - BD = a/2 - a/3 = a/6`
Applying Pythagoras theorem in ΔADE, we get
AD2 = AE2 + DE2
`AD^2 = ((asqrt3)/2)^2 + (a/6)^2`
`= ((3a^2)/4) + (a^2/36)`
`= (28a^2)/36`
`= 7/9 AB^2`
⇒ 9 AD2 = 7 AB2
APPEARS IN
संबंधित प्रश्न
Two towers of heights 10 m and 30 m stand on a plane ground. If the distance between their feet is 15 m, find the distance between their tops
A 15 m long ladder reached a window 12 m high from the ground on placing it against a wall at a distance a. Find the distance of the foot of the ladder from the wall.

Which of the following can be the sides of a right triangle?
2.5 cm, 6.5 cm, 6 cm
In the case of right-angled triangles, identify the right angles.
Identify, with reason, if the following is a Pythagorean triplet.
(3, 5, 4)
M andN are the mid-points of the sides QR and PQ respectively of a PQR, right-angled at Q.
Prove that:
(i) PM2 + RN2 = 5 MN2
(ii) 4 PM2 = 4 PQ2 + QR2
(iii) 4 RN2 = PQ2 + 4 QR2(iv) 4 (PM2 + RN2) = 5 PR2
In ∆ ABC, AD ⊥ BC.
Prove that AC2 = AB2 +BC2 − 2BC x BD
In the figure below, find the value of 'x'.

Find the distance between the helicopter and the ship
Prove that the area of the equilateral triangle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the equilateral triangles drawn on the other two sides of the triangle.
Two poles of 10 m and 15 m stand upright on a plane ground. If the distance between the tops is 13 m, find the distance between their feet.
