Advertisements
Advertisements
प्रश्न
Which of the following can be the sides of a right triangle?
2.5 cm, 6.5 cm, 6 cm
In the case of right-angled triangles, identify the right angles.
उत्तर
2.5 cm, 6.5 cm, 6 cm
(2.5)2 = 6.25
(6.5)2 = 42.25
(6)2 = 36
It can be observed that,
36 + 6.25 = 42.25
(6)2 + (2.5)2 = (6.5)2
The square of the length of one side is the sum of the squares of the lengths of the remaining two sides. Hence, these are the sides of a right-angled triangle. Right angle will be in front of the side of measure 6.5 cm.
APPEARS IN
संबंधित प्रश्न
P and Q are the mid-points of the sides CA and CB respectively of a ∆ABC, right angled at C. Prove that:
`(i) 4AQ^2 = 4AC^2 + BC^2`
`(ii) 4BP^2 = 4BC^2 + AC^2`
`(iii) (4AQ^2 + BP^2 ) = 5AB^2`
PQR is a triangle right angled at P and M is a point on QR such that PM ⊥ QR. Show that PM2 = QM . MR
ABC is an isosceles triangle with AC = BC. If AB2 = 2AC2, prove that ABC is a right triangle.
Tick the correct answer and justify: In ΔABC, AB = `6sqrt3` cm, AC = 12 cm and BC = 6 cm.
The angle B is:
A tree is broken at a height of 5 m from the ground and its top touches the ground at a distance of 12 m from the base of the tree. Find the original height of the tree.
If the angles of a triangle are 30°, 60°, and 90°, then shown that the side opposite to 30° is half of the hypotenuse, and the side opposite to 60° is `sqrt(3)/2` times of the hypotenuse.
In the given figure, BL and CM are medians of a ∆ABC right-angled at A. Prove that 4 (BL2 + CM2) = 5 BC2.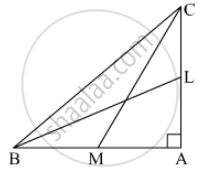
A point OI in the interior of a rectangle ABCD is joined with each of the vertices A, B, C and D. Prove that OB2 + OD2 = OC2 + OA2
In a right angled triangle, if length of hypotenuse is 25 cm and height is 7 cm, then what is the length of its base?
Two poles of 10 m and 15 m stand upright on a plane ground. If the distance between the tops is 13 m, find the distance between their feet.
