Question

P and Q are the mid-points of the sides CA and CB respectively of a ∆ABC, right angled at C. Prove that:

`(i) 4AQ^2 = 4AC^2 + BC^2`

`(ii) 4BP^2 = 4BC^2 + AC^2`

`(iii) (4AQ^2 + BP^2 ) = 5AB^2`

Answer 1

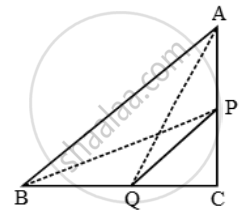
(i) Since ∆AQC is a right triangle right-angled at C.

`∴ AQ^2 = AC^2 + QC^2`

`⇒ 4AQ^2 = 4AC^2 + 4QC^2 `

`⇒ 4AQ^2 = 4AC^2 + (2QC)^2`

`⇒ 4AQ^2 = 4AC^2 + BC^2 `

(ii) Since ∆BPC is a right triangle right-angled at C.

`∴ BP^2 = BC^2 + CP^2`

`⇒ 4BP^2 = 4BC^2 + 4CP^2 `

`⇒ 4BP^2 = 4BC^2 + (2CP)^2`

`⇒ 4BP^2 = 4BC^2 + AC^2 [∵ AC = 2CP]`

(iii) From (i) and (ii), we have

`4AQ^2 = 4AC^2 + BC^2 and, 4BC^2 = 4BC^2 + AC^2`

`∴ 4AQ^2 + 4BP^2 = (4AC^2 + BC^2 ) + (4BC^2 + AC^2 )`

`⇒ 4(AQ^2 + BP^2 ) = 5 (AC^2 + BC^2 )`

`⇒ 4(AQ^2 + BP^2 ) = 5 AB^2`

[In ∆ABC, we have AB² = AC² + BC² ]