Advertisements
Advertisements
प्रश्न
A tree is broken at a height of 5 m from the ground and its top touches the ground at a distance of 12 m from the base of the tree. Find the original height of the tree.
उत्तर
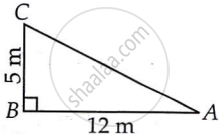
In the given figure, BC represents the unbroken part of the tree. Point C represents the point where the tree broke and CA represents the broken part of the tree. Triangle ABC, thus formed, is right-angled at B.
Applying Pythagoras theorem in ΔABC,
AC2 = BC2 + AB2
AC2 = (5 m)2 + (12 m)2
AC2 = 25 m2 + 144 m2
AC2 = 169 m2
AC = 13 m
Thus, original height of the tree = AC + CB
= 13 m + 5 m
= 18 m
APPEARS IN
संबंधित प्रश्न
Sides of triangle are given below. Determine it is a right triangle or not? In case of a right triangle, write the length of its hypotenuse. 50 cm, 80 cm, 100 cm
In Figure, ABD is a triangle right angled at A and AC ⊥ BD. Show that AD2 = BD × CD

In ∆ABC, seg AD ⊥ seg BC, DB = 3CD.
Prove that: 2AB2 = 2AC2 + BC2

In the given figure, ∠B = 90°, XY || BC, AB = 12 cm, AY = 8cm and AX : XB = 1 : 2 = AY : YC.
Find the lengths of AC and BC.

In the following figure, OP, OQ, and OR are drawn perpendiculars to the sides BC, CA and AB respectively of triangle ABC.
Prove that: AR2 + BP2 + CQ2 = AQ2 + CP2 + BR2

O is any point inside a rectangle ABCD.
Prove that: OB2 + OD2 = OC2 + OA2.
In the following Figure ∠ACB= 90° and CD ⊥ AB, prove that CD2 = BD × AD

The foot of a ladder is 6m away from a wall and its top reaches a window 8m above the ground. If the ladder is shifted in such a way that its foot is 8m away from the wall to what height does its tip reach?
In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AC2 = AD2 + BC x DE + `(1)/(4)"BC"^2`
A 5 m long ladder is placed leaning towards a vertical wall such that it reaches the wall at a point 4 m high. If the foot of the ladder is moved 1.6 m towards the wall, then find the distance by which the top of the ladder would slide upwards on the wall.
