Advertisements
Advertisements
प्रश्न
A tree is broken at a height of 5 m from the ground and its top touches the ground at a distance of 12 m from the base of the tree. Find the original height of the tree.
उत्तर
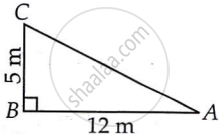
In the given figure, BC represents the unbroken part of the tree. Point C represents the point where the tree broke and CA represents the broken part of the tree. Triangle ABC, thus formed, is right-angled at B.
Applying Pythagoras theorem in ΔABC,
AC2 = BC2 + AB2
AC2 = (5 m)2 + (12 m)2
AC2 = 25 m2 + 144 m2
AC2 = 169 m2
AC = 13 m
Thus, original height of the tree = AC + CB
= 13 m + 5 m
= 18 m
APPEARS IN
संबंधित प्रश्न
The diagonal of a rectangular field is 16 metres more than the shorter side. If the longer side is 14 metres more than the shorter side, then find the lengths of the sides of the field.
P and Q are the mid-points of the sides CA and CB respectively of a ∆ABC, right angled at C. Prove that:
`(i) 4AQ^2 = 4AC^2 + BC^2`
`(ii) 4BP^2 = 4BC^2 + AC^2`
`(iii) (4AQ^2 + BP^2 ) = 5AB^2`
Sides of triangle are given below. Determine it is a right triangle or not? In case of a right triangle, write the length of its hypotenuse. 13 cm, 12 cm, 5 cm
Walls of two buildings on either side of a street are parallel to each other. A ladder 5.8 m long is placed on the street such that its top just reaches the window of a building at the height of 4 m. On turning the ladder over to the other side of the street, its top touches the window of the other building at a height 4.2 m. Find the width of the street.
Two poles of heights 6 m and 11 m stand vertically on a plane ground. If the distance between their feet is 12 m;
find the distance between their tips.
The sides of the triangle are given below. Find out which one is the right-angled triangle?
40, 20, 30
From a point O in the interior of aΔABC, perpendicular OD, OE and OF are drawn to the sides BC, CA and AB respectively. Prove that: AF2 + BD2 + CE2 = OA2 + OB2 + OC2 - OD2 - OE2 - OF2
In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AB2 = AD2 - BC x CE + `(1)/(4)"BC"^2`
In a right-angled triangle ABC,ABC = 90°, AC = 10 cm, BC = 6 cm and BC produced to D such CD = 9 cm. Find the length of AD.
Determine whether the triangle whose lengths of sides are 3 cm, 4 cm, 5 cm is a right-angled triangle.
