Advertisements
Advertisements
प्रश्न
In a right-angled triangle ABC,ABC = 90°, AC = 10 cm, BC = 6 cm and BC produced to D such CD = 9 cm. Find the length of AD.
उत्तर
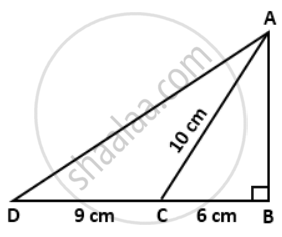
In ΔABC, ∠B = 90°
∴ AC2 = AB2 + BC2 ....(Pythagoras Theorem)
⇒ 102 = AB2 + 62
⇒ AB2 = 102 - 62
= 100 - 36
= 64
Now,
BD = BC + CD
= 6 + 9
= 15cm
⇒ BD2 = 225
In ΔABD, ∠B = 90°
∴ AD2 = AB2 + BD2
⇒ AD2 = 64 + 225 = 289
⇒ AD = 17cm.
APPEARS IN
संबंधित प्रश्न
In the following figure, O is a point in the interior of a triangle ABC, OD ⊥ BC, OE ⊥ AC and OF ⊥ AB. Show that

(i) OA2 + OB2 + OC2 − OD2 − OE2 − OF2 = AF2 + BD2 + CE2
(ii) AF2 + BD2 + CE2 = AE2 + CD2 + BF2
In the given figure, ABC is a triangle in which ∠ABC> 90° and AD ⊥ CB produced. Prove that AC2 = AB2 + BC2 + 2BC.BD.

Prove that the sum of the squares of the diagonals of parallelogram is equal to the sum of the squares of its sides.
ABC is a triangle right angled at C. If AB = 25 cm and AC = 7 cm, find BC.
In a trapezium ABCD, seg AB || seg DC seg BD ⊥ seg AD, seg AC ⊥ seg BC, If AD = 15, BC = 15 and AB = 25. Find A(▢ABCD)

A man goes 40 m due north and then 50 m due west. Find his distance from the starting point.
In triangle ABC, angle A = 90o, CA = AB and D is the point on AB produced.
Prove that DC2 - BD2 = 2AB.AD.
In equilateral Δ ABC, AD ⊥ BC and BC = x cm. Find, in terms of x, the length of AD.
Show that the triangle ABC is a right-angled triangle; if: AB = 9 cm, BC = 40 cm and AC = 41 cm
Use the information given in the figure to find the length AD.

The sides of the triangle are given below. Find out which one is the right-angled triangle?
8, 15, 17
A ladder 25m long reaches a window of a building 20m above the ground. Determine the distance of the foot of the ladder from the building.
The foot of a ladder is 6m away from a wall and its top reaches a window 8m above the ground. If the ladder is shifted in such a way that its foot is 8m away from the wall to what height does its tip reach?
Two poles of height 9m and 14m stand on a plane ground. If the distance between their 12m, find the distance between their tops.
In a triangle ABC right angled at C, P and Q are points of sides CA and CB respectively, which divide these sides the ratio 2 : 1.
Prove that: 9AQ2 = 9AC2 + 4BC2
In a triangle ABC right angled at C, P and Q are points of sides CA and CB respectively, which divide these sides the ratio 2 : 1.
Prove that : 9(AQ2 + BP2) = 13AB2
Is the triangle with sides 25 cm, 5 cm and 24 cm a right triangle? Give reasons for your answer.
If the areas of two circles are the same, they are congruent.
The foot of a ladder is 6 m away from its wall and its top reaches a window 8 m above the ground. Find the length of the ladder.
The foot of a ladder is 6 m away from its wall and its top reaches a window 8 m above the ground. If the ladder is shifted in such a way that its foot is 8 m away from the wall, to what height does its top reach?
