Advertisements
Advertisements
प्रश्न
In a right-angled triangle ABC,ABC = 90°, AC = 10 cm, BC = 6 cm and BC produced to D such CD = 9 cm. Find the length of AD.
उत्तर
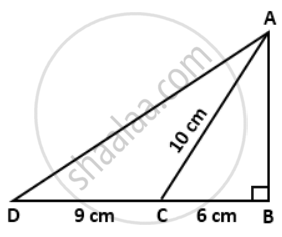
In ΔABC, ∠B = 90°
∴ AC2 = AB2 + BC2 ....(Pythagoras Theorem)
⇒ 102 = AB2 + 62
⇒ AB2 = 102 - 62
= 100 - 36
= 64
Now,
BD = BC + CD
= 6 + 9
= 15cm
⇒ BD2 = 225
In ΔABD, ∠B = 90°
∴ AD2 = AB2 + BD2
⇒ AD2 = 64 + 225 = 289
⇒ AD = 17cm.
APPEARS IN
संबंधित प्रश्न
The points A(4, 7), B(p, 3) and C(7, 3) are the vertices of a right traingle ,right-angled at B. Find the values of p.
If ABC is an equilateral triangle of side a, prove that its altitude = ` \frac { \sqrt { 3 } }{ 2 } a`
ABC is a right-angled triangle, right-angled at A. A circle is inscribed in it. The lengths of the two sides containing the right angle are 5 cm and 12 cm. Find the radius of the circle
ABCD is a rhombus. Prove that AB2 + BC2 + CD2 + DA2= AC2 + BD2
ABC is a triangle right angled at C. If AB = 25 cm and AC = 7 cm, find BC.
The given figure shows a quadrilateral ABCD in which AD = 13 cm, DC = 12 cm, BC = 3 cm and ∠ABD = ∠BCD = 90o. Calculate the length of AB.
In an isosceles triangle ABC; AB = AC and D is the point on BC produced.
Prove that: AD2 = AC2 + BD.CD.
In the given figure, angle BAC = 90°, AC = 400 m, and AB = 300 m. Find the length of BC.

In the given figure, angle ACP = ∠BDP = 90°, AC = 12 m, BD = 9 m and PA= PB = 15 m. Find:
(i) CP
(ii) PD
(iii) CD

In the figure below, find the value of 'x'.

Find the Pythagorean triplet from among the following set of numbers.
2, 4, 5
The sides of the triangle are given below. Find out which one is the right-angled triangle?
1.5, 1.6, 1.7
A man goes 10 m due east and then 24 m due north. Find the distance from the straight point.
In a right-angled triangle PQR, right-angled at Q, S and T are points on PQ and QR respectively such as PT = SR = 13 cm, QT = 5 cm and PS = TR. Find the length of PQ and PS.
Find the length of the support cable required to support the tower with the floor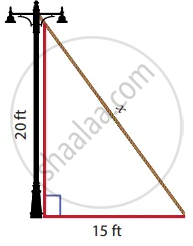
In the figure, find AR
In a right angled triangle, if length of hypotenuse is 25 cm and height is 7 cm, then what is the length of its base?
If ΔABC ~ ΔPQR, `("ar" triangle "ABC")/("ar" triangle "PQR") = 9/4` and AB = 18 cm, then the length of PQ is ______.
A right-angled triangle may have all sides equal.
Points A and B are on the opposite edges of a pond as shown in figure. To find the distance between the two points, the surveyor makes a right-angled triangle as shown. Find the distance AB.

