Advertisements
Advertisements
प्रश्न
In the given figure, PQ = `"RS"/(3)` = 8cm, 3ST = 4QT = 48cm.
SHow that ∠RTP = 90°.
उत्तर
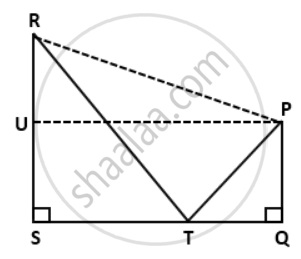
PQ = `"RS"/(3)` = 8cm
⇒ PQ = 8cm and RS = 3 x 8 = 24cm
3ST = 4QT = 48cm
⇒ ST = `(48)/(3) = 16"cm" and "QT" = (48)/(4)` = 12cm
In ΔPTQ,
PT2 = PQ2 + QT2
= 82 + 122
= 64 + 144
= 208
In ΔRTS,
RT2 = RS2 + ST2
= 242 + 162
= 576 + 256
= 832
Now, PT2 + RT2
= 208 + 832
= 1040 .....(i)
Draw PU ⊥ RS and Join PR.
PU = SQ
= ST + TQ
= 16 + 12
= 28cm
RU = RS - US
= RS - PQ
= 24 - 8
= 16cm
In ΔRUP,
PR2 = RU2 + PU2
= 162 + 282
= 256 + 784
= 1040 ....(ii)
From (i) and (ii), we get
PT2 + RT2 = PR2
Thus, ∠RTP = 90°.
APPEARS IN
संबंधित प्रश्न
In a right triangle ABC, right-angled at B, BC = 12 cm and AB = 5 cm. The radius of the circle inscribed in the triangle (in cm) is
(A) 4
(B) 3
(C) 2
(D) 1
Two towers of heights 10 m and 30 m stand on a plane ground. If the distance between their feet is 15 m, find the distance between their tops
Sides of triangles are given below. Determine it is a right triangles? In case of a right triangle, write the length of its hypotenuse. 3 cm, 8 cm, 6 cm
Prove that the sum of the squares of the sides of a rhombus is equal to the sum of the squares of its diagonals
Which of the following can be the sides of a right triangle?
1.5 cm, 2 cm, 2.5 cm
In the case of right-angled triangles, identify the right angles.
Pranali and Prasad started walking to the East and to the North respectively, from the same point and at the same speed. After 2 hours distance between them was \[15\sqrt{2}\]
km. Find their speed per hour.
In the following figure, AD is perpendicular to BC and D divides BC in the ratio 1: 3.
Prove that : 2AC2 = 2AB2 + BC2
In the following figure, OP, OQ, and OR are drawn perpendiculars to the sides BC, CA and AB respectively of triangle ABC.
Prove that: AR2 + BP2 + CQ2 = AQ2 + CP2 + BR2

Find the length of diagonal of the square whose side is 8 cm.
In ∆ ABC, AD ⊥ BC.
Prove that AC2 = AB2 +BC2 − 2BC x BD
Triangle XYZ is right-angled at vertex Z. Calculate the length of YZ, if XY = 13 cm and XZ = 12 cm.
The sides of the triangle are given below. Find out which one is the right-angled triangle?
11, 12, 15
The sides of the triangle are given below. Find out which one is the right-angled triangle?
1.5, 1.6, 1.7
Find the length of the hypotenuse of a triangle whose other two sides are 24cm and 7cm.
A right triangle has hypotenuse p cm and one side q cm. If p - q = 1, find the length of third side of the triangle.
In a triangle ABC right angled at C, P and Q are points of sides CA and CB respectively, which divide these sides the ratio 2 : 1.
Prove that: 9BP2 = 9BC2 + 4AC2
A man goes 18 m due east and then 24 m due north. Find the distance of his current position from the starting point?
If ΔABC ~ ΔPQR, `("ar" triangle "ABC")/("ar" triangle "PQR") = 9/4` and AB = 18 cm, then the length of PQ is ______.
Is the triangle with sides 25 cm, 5 cm and 24 cm a right triangle? Give reasons for your answer.
Prove that the area of the equilateral triangle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the equilateral triangles drawn on the other two sides of the triangle.
