Advertisements
Advertisements
प्रश्न
In a triangle ABC right angled at C, P and Q are points of sides CA and CB respectively, which divide these sides the ratio 2 : 1.
Prove that : 9(AQ2 + BP2) = 13AB2
उत्तर
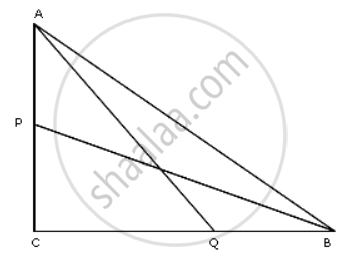
P divides AC in the ratio 2 : 1
So C.P. = `(2)/(3) "AC"` .......(i)
Q divides BC in the ratio 2 : 1
QC = `(2)/(3)"BC"` ......(ii)
Adding (iii) and (iv), we get
9(AQ2 + BP2) = 13(BC2 + AC2)
⇒ 9(AQ2 + BP2) = 13AB2.
APPEARS IN
संबंधित प्रश्न
In figure, ∠B of ∆ABC is an acute angle and AD ⊥ BC, prove that AC2 = AB2 + BC2 – 2BC × BD
Nazima is fly fishing in a stream. The tip of her fishing rod is 1.8 m above the surface of the water and the fly at the end of the string rests on the water 3.6 m away and 2.4 m from a point directly under the tip of the rod. Assuming that her string (from the tip of her rod to the fly) is taut, ho much string does she have out (see Figure)? If she pulls in the string at the rate of 5 cm per second, what will be the horizontal distance of the fly from her after 12 seconds?

Prove that the points A(0, −1), B(−2, 3), C(6, 7) and D(8, 3) are the vertices of a rectangle ABCD?
Some question and their alternative answer are given. Select the correct alternative.
If a, b, and c are sides of a triangle and a2 + b2 = c2, name the type of triangle.
A man goes 40 m due north and then 50 m due west. Find his distance from the starting point.
In triangle ABC, angle A = 90o, CA = AB and D is the point on AB produced.
Prove that DC2 - BD2 = 2AB.AD.
Prove that `(sin θ + cosec θ)^2 + (cos θ + sec θ)^2 = 7 + tan^2 θ + cot^2 θ`.
In the given figure, angle ADB = 90°, AC = AB = 26 cm and BD = DC. If the length of AD = 24 cm; find the length of BC.

A boy first goes 5 m due north and then 12 m due east. Find the distance between the initial and the final position of the boy.
Find the Pythagorean triplet from among the following set of numbers.
3, 4, 5
The sides of the triangle are given below. Find out which one is the right-angled triangle?
11, 60, 61
In a right-angled triangle ABC,ABC = 90°, AC = 10 cm, BC = 6 cm and BC produced to D such CD = 9 cm. Find the length of AD.
In a right-angled triangle PQR, right-angled at Q, S and T are points on PQ and QR respectively such as PT = SR = 13 cm, QT = 5 cm and PS = TR. Find the length of PQ and PS.
The perpendicular PS on the base QR of a ∆PQR intersects QR at S, such that QS = 3 SR. Prove that 2PQ2 = 2PR2 + QR2
In a right angled triangle, the hypotenuse is the greatest side
In triangle ABC, line I, is a perpendicular bisector of BC.
If BC = 12 cm, SM = 8 cm, find CS
In the figure, find AR
Prove that the area of the equilateral triangle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the equilateral triangles drawn on the other two sides of the triangle.
In an isosceles triangle PQR, the length of equal sides PQ and PR is 13 cm and base QR is 10 cm. Find the length of perpendicular bisector drawn from vertex P to side QR.
Two circles having same circumference are congruent.
