Advertisements
Advertisements
Question
In a triangle ABC right angled at C, P and Q are points of sides CA and CB respectively, which divide these sides the ratio 2 : 1.
Prove that : 9(AQ2 + BP2) = 13AB2
Solution
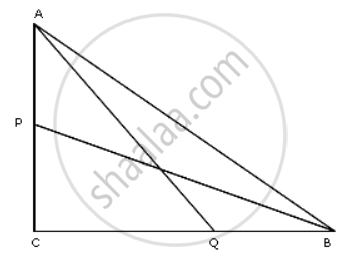
P divides AC in the ratio 2 : 1
So C.P. = `(2)/(3) "AC"` .......(i)
Q divides BC in the ratio 2 : 1
QC = `(2)/(3)"BC"` ......(ii)
Adding (iii) and (iv), we get
9(AQ2 + BP2) = 13(BC2 + AC2)
⇒ 9(AQ2 + BP2) = 13AB2.
APPEARS IN
RELATED QUESTIONS
ABCD is a rhombus. Prove that AB2 + BC2 + CD2 + DA2= AC2 + BD2
ABC is a right triangle right-angled at C. Let BC = a, CA = b, AB = c and let p be the length of perpendicular from C on AB, prove that
(i) cp = ab
`(ii) 1/p^2=1/a^2+1/b^2`
In Figure, ABD is a triangle right angled at A and AC ⊥ BD. Show that AD2 = BD × CD

In the following figure, O is a point in the interior of a triangle ABC, OD ⊥ BC, OE ⊥ AC and OF ⊥ AB. Show that

(i) OA2 + OB2 + OC2 − OD2 − OE2 − OF2 = AF2 + BD2 + CE2
(ii) AF2 + BD2 + CE2 = AE2 + CD2 + BF2
A 15 m long ladder reached a window 12 m high from the ground on placing it against a wall at a distance a. Find the distance of the foot of the ladder from the wall.

Which of the following can be the sides of a right triangle?
2.5 cm, 6.5 cm, 6 cm
In the case of right-angled triangles, identify the right angles.
Identify, with reason, if the following is a Pythagorean triplet.
(5, 12, 13)
Find the length diagonal of a rectangle whose length is 35 cm and breadth is 12 cm.
In the given figure, M is the midpoint of QR. ∠PRQ = 90°. Prove that, PQ2 = 4PM2 – 3PR2.


In ΔMNP, ∠MNP = 90˚, seg NQ ⊥ seg MP, MQ = 9, QP = 4, find NQ.
A ladder 13 m long rests against a vertical wall. If the foot of the ladder is 5 m from the foot of the wall, find the distance of the other end of the ladder from the ground.
In the following figure, OP, OQ, and OR are drawn perpendiculars to the sides BC, CA and AB respectively of triangle ABC.
Prove that: AR2 + BP2 + CQ2 = AQ2 + CP2 + BR2

In the given figure, angle BAC = 90°, AC = 400 m, and AB = 300 m. Find the length of BC.

The sides of the triangle are given below. Find out which one is the right-angled triangle?
11, 60, 61
Calculate the area of a right-angled triangle whose hypotenuse is 65cm and one side is 16cm.
In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AC2 = AD2 + BC x DE + `(1)/(4)"BC"^2`
In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AC2 - AB2 = 2BC x ED
In a right-angled triangle ABC,ABC = 90°, AC = 10 cm, BC = 6 cm and BC produced to D such CD = 9 cm. Find the length of AD.
A flag pole 18 m high casts a shadow 9.6 m long. Find the distance of the top of the pole from the far end of the shadow.
Two angles are said to be ______, if they have equal measures.
