Advertisements
Advertisements
Question
A ladder 13 m long rests against a vertical wall. If the foot of the ladder is 5 m from the foot of the wall, find the distance of the other end of the ladder from the ground.
Solution
The pictorial representation of the given problem is given below,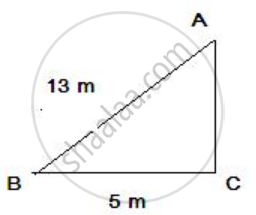
Pythagoras theorem states that in a right-angled triangle, the square on the hypotenuse is equal to the sum of the squares on the remaining two sides.
Here, AB is the hypotenuse.
Therefore applying the Pythagoras theorem we get,
AB2 = BC2 + CA2
132 = 52 + CA2
CA2 = 132 - 52
CA2 = 144
CA = 12 m
Therefore, the distance of the other end of the ladder from the ground is 12m.
APPEARS IN
RELATED QUESTIONS
In a ∆ABC, AD ⊥ BC and AD2 = BC × CD. Prove ∆ABC is a right triangle
ABC is a right triangle right-angled at C. Let BC = a, CA = b, AB = c and let p be the length of perpendicular from C on AB, prove that
(i) cp = ab
`(ii) 1/p^2=1/a^2+1/b^2`
PQR is a triangle right angled at P and M is a point on QR such that PM ⊥ QR. Show that PM2 = QM . MR
A ladder 10 m long reaches a window 8 m above the ground. Find the distance of the foot of the ladder from base of the wall.
Prove that the sum of the squares of the diagonals of parallelogram is equal to the sum of the squares of its sides.
In the given figure, ∆ABC is an equilateral triangle of side 3 units. Find the coordinates of the other two vertices ?

Identify, with reason, if the following is a Pythagorean triplet.
(5, 12, 13)
In the given figure, ∠DFE = 90°, FG ⊥ ED, If GD = 8, FG = 12, find (1) EG (2) FD and (3) EF

The given figure shows a quadrilateral ABCD in which AD = 13 cm, DC = 12 cm, BC = 3 cm and ∠ABD = ∠BCD = 90o. Calculate the length of AB.
Find the Pythagorean triplet from among the following set of numbers.
2, 6, 7
Find the length of the hypotenuse of a triangle whose other two sides are 24cm and 7cm.
Each side of rhombus is 10cm. If one of its diagonals is 16cm, find the length of the other diagonals.
In a triangle ABC right angled at C, P and Q are points of sides CA and CB respectively, which divide these sides the ratio 2 : 1.
Prove that: 9AQ2 = 9AC2 + 4BC2
In a square PQRS of side 5 cm, A, B, C and D are points on sides PQ, QR, RS and SP respectively such as PA = PD = RB = RC = 2 cm. Prove that ABCD is a rectangle. Also, find the area and perimeter of the rectangle.
Determine whether the triangle whose lengths of sides are 3 cm, 4 cm, 5 cm is a right-angled triangle.
There are two paths that one can choose to go from Sarah’s house to James's house. One way is to take C street, and the other way requires to take B street and then A street. How much shorter is the direct path along C street?

The perpendicular PS on the base QR of a ∆PQR intersects QR at S, such that QS = 3 SR. Prove that 2PQ2 = 2PR2 + QR2
Find the unknown side in the following triangles
Find the distance between the helicopter and the ship
If the areas of two circles are the same, they are congruent.
