Advertisements
Advertisements
Question
The given figure shows a quadrilateral ABCD in which AD = 13 cm, DC = 12 cm, BC = 3 cm and ∠ABD = ∠BCD = 90o. Calculate the length of AB.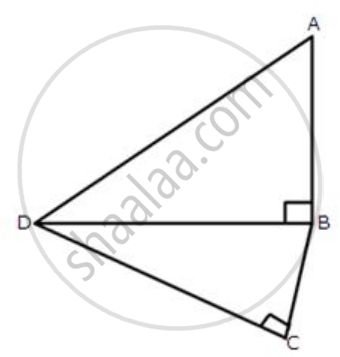
Solution
Pythagoras theorem states that in a right-angled triangle, the square on the hypotenuse is equal to the sum of the squares on the remaining two sides.
First, we consider the ΔBDC and applying Pythagoras theorem we get,
DB2 = DC2 + BC2
DB2 = 122 + 32
DB2 = 144 + 9
DB2 = 153
Now, we consider the ΔABD and applying Pythagoras theorem we get,
DA2 = DB2 + BA2
132 = 153 + BA2
BA2 = 169 - 153
BA = 4
The length of AB is 4 cm.
APPEARS IN
RELATED QUESTIONS
P and Q are the mid-points of the sides CA and CB respectively of a ∆ABC, right angled at C. Prove that:
`(i) 4AQ^2 = 4AC^2 + BC^2`
`(ii) 4BP^2 = 4BC^2 + AC^2`
`(iii) (4AQ^2 + BP^2 ) = 5AB^2`
In a ∆ABC, AD ⊥ BC and AD2 = BC × CD. Prove ∆ABC is a right triangle
In Figure, ABD is a triangle right angled at A and AC ⊥ BD. Show that AD2 = BD × CD
The diagonals of a rhombus measure 16 cm and 30 cm. Find its perimeter.
In the given figure, ∆ABC is an equilateral triangle of side 3 units. Find the coordinates of the other two vertices ?
Prove that the points A(0, −1), B(−2, 3), C(6, 7) and D(8, 3) are the vertices of a rectangle ABCD?
Identify, with reason, if the following is a Pythagorean triplet.
(5, 12, 13)
Pranali and Prasad started walking to the East and to the North respectively, from the same point and at the same speed. After 2 hours distance between them was \[15\sqrt{2}\]
km. Find their speed per hour.
In a quadrilateral ABCD, ∠B = 90° and ∠D = 90°.
Prove that: 2AC2 - AB2 = BC2 + CD2 + DA2
In the given figure, AD = 13 cm, BC = 12 cm, AB = 3 cm and angle ACD = angle ABC = 90°. Find the length of DC.
A ladder, 6.5 m long, rests against a vertical wall. If the foot of the ladder is 2.5 m from the foot of the wall, find up to how much height does the ladder reach?
In the right-angled ∆PQR, ∠ P = 90°. If l(PQ) = 24 cm and l(PR) = 10 cm, find the length of seg QR.
In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AB2 + AC2 = 2(AD2 + CD2)
In a right-angled triangle PQR, right-angled at Q, S and T are points on PQ and QR respectively such as PT = SR = 13 cm, QT = 5 cm and PS = TR. Find the length of PQ and PS.
A man goes 18 m due east and then 24 m due north. Find the distance of his current position from the starting point?
Find the length of the support cable required to support the tower with the floor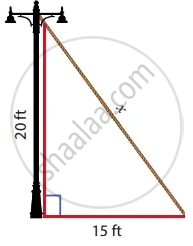
If S is a point on side PQ of a ΔPQR such that PS = QS = RS, then ______.
Two rectangles are congruent, if they have same ______ and ______.
In a triangle, sum of squares of two sides is equal to the square of the third side.
