Advertisements
Advertisements
Question
The diagonals of a rhombus measure 16 cm and 30 cm. Find its perimeter.
Solution
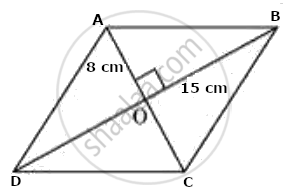
Let ABCD be a rhombus (all sides are of equal length) and its diagonals, AC and BD, are intersecting each other at point O. Diagonals in a rhombus bisect each other at 90°. It can be observed that
AO = `(AC)/2`
= `16/2`
= 8 cm
BO = `(BD)/2`
= `30/2`
= 15 cm
By applying Pythagoras theorem in ΔAOB,
OA2 + OB2 = AB2
82 + 152 = AB2
64 + 225 = AB2
289 = AB2
AB = 17
Therefore, the length of the side of rhombus is 17 cm.
Perimeter of rhombus = 4 × Side of the rhombus
= 4 × 17
= 68 cm
APPEARS IN
RELATED QUESTIONS
ABC is a right-angled triangle, right-angled at A. A circle is inscribed in it. The lengths of the two sides containing the right angle are 5 cm and 12 cm. Find the radius of the circle
In Figure, ABD is a triangle right angled at A and AC ⊥ BD. Show that AD2 = BD × CD

In an equilateral triangle ABC, D is a point on side BC such that BD = `1/3BC` . Prove that 9 AD2 = 7 AB2
A 15 m long ladder reached a window 12 m high from the ground on placing it against a wall at a distance a. Find the distance of the foot of the ladder from the wall.

For finding AB and BC with the help of information given in the figure, complete following activity.
AB = BC .......... 
∴ ∠BAC = 
∴ AB = BC =  × AC
× AC
=  × `sqrt8`
× `sqrt8`
=  × `2sqrt2`
× `2sqrt2`
= 

In triangle ABC, ∠B = 90o and D is the mid-point of BC.
Prove that: AC2 = AD2 + 3CD2.
Show that the triangle ABC is a right-angled triangle; if: AB = 9 cm, BC = 40 cm and AC = 41 cm
A right triangle has hypotenuse p cm and one side q cm. If p - q = 1, find the length of third side of the triangle.
In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AB2 + AC2 = 2(AD2 + CD2)
A flag pole 18 m high casts a shadow 9.6 m long. Find the distance of the top of the pole from the far end of the shadow.
