Advertisements
Advertisements
Question
In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AB2 + AC2 = 2(AD2 + CD2)
Solution
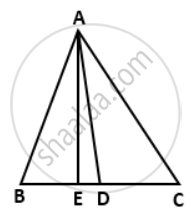
We have ∠AED = 90°
∴ ∠ADE < 90° and ∠ADC > 90°
i.e. ∠ADE is acute and ∠ADC is obtuse.
From (iii), we have
AB2 + AC2 = `2"AD"^2 + (1)/(2)"BC"^2`
⇒ AB2 + AC2 = `2"AD"^2 + (1)/(2)(2 xx "CD")^2`
⇒ AB2 + AC2 = `2"AD"^2 + (1)/(2) xx 4"CD"^2`
⇒ AB2 + AC2 = 2AD2 + 2CD2
⇒ AB2 + AC2 = 2(AD2 + CD2).
APPEARS IN
RELATED QUESTIONS
Two towers of heights 10 m and 30 m stand on a plane ground. If the distance between their feet is 15 m, find the distance between their tops
In a ∆ABC, AD ⊥ BC and AD2 = BC × CD. Prove ∆ABC is a right triangle
ABC is an equilateral triangle of side 2a. Find each of its altitudes.
D and E are points on the sides CA and CB respectively of a triangle ABC right angled at C. Prove that AE2 + BD2 = AB2 + DE2
Prove that, in a right-angled triangle, the square of the hypotenuse is equal to the sum of the square of remaining two sides
Identify, with reason, if the following is a Pythagorean triplet.
(5, 12, 13)
Pranali and Prasad started walking to the East and to the North respectively, from the same point and at the same speed. After 2 hours distance between them was \[15\sqrt{2}\]
km. Find their speed per hour.
In right angle ΔABC, if ∠B = 90°, AB = 6, BC = 8, then find AC.
In the figure, given below, AD ⊥ BC.
Prove that: c2 = a2 + b2 - 2ax.
In an isosceles triangle ABC; AB = AC and D is the point on BC produced.
Prove that: AD2 = AC2 + BD.CD.
In triangle PQR, angle Q = 90°, find: PQ, if PR = 34 cm and QR = 30 cm
The sides of the triangle are given below. Find out which one is the right-angled triangle?
1.5, 1.6, 1.7
Find the length of the perpendicular of a triangle whose base is 5cm and the hypotenuse is 13cm. Also, find its area.
In the given figure. PQ = PS, P =R = 90°. RS = 20 cm and QR = 21 cm. Find the length of PQ correct to two decimal places.
If in a ΔPQR, PR2 = PQ2 + QR2, then the right angle of ∆PQR is at the vertex ________
Find the unknown side in the following triangles
In a right angled triangle, if length of hypotenuse is 25 cm and height is 7 cm, then what is the length of its base?
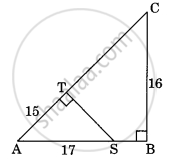
In the given figure, ∠T and ∠B are right angles. If the length of AT, BC and AS (in centimeters) are 15, 16, and 17 respectively, then the length of TC (in centimeters) is ______.
In the given figure, AD is a median of a triangle ABC and AM ⊥ BC. Prove that:

(i) `"AC"^2 = "AD"^2 + "BC"."DM" + (("BC")/2)^2`
(ii) `"AB"^2 = "AD"^2 - "BC"."DM" + (("BC")/2)^2`
(iii) `"AC"^2 + "AB"^2 = 2"AD"^2 + 1/2"BC"^2`
