Advertisements
Advertisements
प्रश्न
In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AB2 + AC2 = 2(AD2 + CD2)
उत्तर
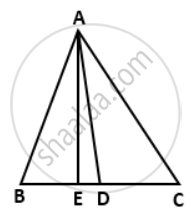
We have ∠AED = 90°
∴ ∠ADE < 90° and ∠ADC > 90°
i.e. ∠ADE is acute and ∠ADC is obtuse.
From (iii), we have
AB2 + AC2 = `2"AD"^2 + (1)/(2)"BC"^2`
⇒ AB2 + AC2 = `2"AD"^2 + (1)/(2)(2 xx "CD")^2`
⇒ AB2 + AC2 = `2"AD"^2 + (1)/(2) xx 4"CD"^2`
⇒ AB2 + AC2 = 2AD2 + 2CD2
⇒ AB2 + AC2 = 2(AD2 + CD2).
APPEARS IN
संबंधित प्रश्न
PQR is a triangle right angled at P and M is a point on QR such that PM ⊥ QR. Show that PM2 = QM . MR
ABC is an equilateral triangle of side 2a. Find each of its altitudes.
In the following figure, O is a point in the interior of a triangle ABC, OD ⊥ BC, OE ⊥ AC and OF ⊥ AB. Show that

(i) OA2 + OB2 + OC2 − OD2 − OE2 − OF2 = AF2 + BD2 + CE2
(ii) AF2 + BD2 + CE2 = AE2 + CD2 + BF2
A ladder 10 m long reaches a window 8 m above the ground. Find the distance of the foot of the ladder from base of the wall.
In the given figure, AD is a median of a triangle ABC and AM ⊥ BC. Prove that:

`"AC"^2 = "AD"^2 + "BC"."DM" + (("BC")/2)^2`
Prove that the sum of the squares of the diagonals of parallelogram is equal to the sum of the squares of its sides.
The diagonals of a rhombus measure 16 cm and 30 cm. Find its perimeter.
In right angle ΔABC, if ∠B = 90°, AB = 6, BC = 8, then find AC.
A man goes 40 m due north and then 50 m due west. Find his distance from the starting point.
In the figure, given below, AD ⊥ BC.
Prove that: c2 = a2 + b2 - 2ax.
Choose the correct alternative:
In right-angled triangle PQR, if hypotenuse PR = 12 and PQ = 6, then what is the measure of ∠P?
In the figure below, find the value of 'x'.

Calculate the area of a right-angled triangle whose hypotenuse is 65cm and one side is 16cm.
The foot of a ladder is 6m away from a wall and its top reaches a window 8m above the ground. If the ladder is shifted in such a way that its foot is 8m away from the wall to what height does its tip reach?
Find the distance between the helicopter and the ship
Choose the correct alternative:
If length of sides of a triangle are a, b, c and a2 + b2 = c2, then which type of triangle it is?
A flag pole 18 m high casts a shadow 9.6 m long. Find the distance of the top of the pole from the far end of the shadow.
Prove that the area of the semicircle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the semicircles drawn on the other two sides of the triangle.
In a right-angled triangle ABC, if angle B = 90°, BC = 3 cm and AC = 5 cm, then the length of side AB is ______.
Two squares are congruent, if they have same ______.
