Advertisements
Advertisements
प्रश्न
PQR is a triangle right angled at P and M is a point on QR such that PM ⊥ QR. Show that PM2 = QM . MR
उत्तर
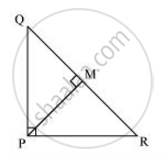
Let ∠MPR = x
In ΔMPR
∠MPR = 180º- 90º - x
∠MRP = 90º - x
Similarity, in ΔMPQ
∠MPQ = 90º - ∠MPR
= 90º - x
∠MQP = 180º - 90º - (90º - x)
∠MQP = x
In ΔQMP and ΔPMR
∠MPQ = ∠MRP
∠PMQ = ∠RMP
∠MQP = ∠MPR
∴ΔQMP ~ ΔPMR (By AAA Similarity criterion)
`=>(QM)/(PM) = (MP)/(MR)`
=>PM2 = QM x MR
APPEARS IN
संबंधित प्रश्न
The points A(4, 7), B(p, 3) and C(7, 3) are the vertices of a right traingle ,right-angled at B. Find the values of p.
In triangle ABC, AB = AC and BD is perpendicular to AC.
Prove that: BD2 - CD2 = 2CD × AD
In figure AB = BC and AD is perpendicular to CD.
Prove that: AC2 = 2BC. DC.
O is any point inside a rectangle ABCD.
Prove that: OB2 + OD2 = OC2 + OA2.
Prove that (1 + cot A - cosec A ) (1 + tan A + sec A) = 2
Calculate the area of a right-angled triangle whose hypotenuse is 65cm and one side is 16cm.
In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AB2 + AC2 = 2(AD2 + CD2)
Lengths of sides of a triangle are 3 cm, 4 cm and 5 cm. The triangle is ______.
Two trees 7 m and 4 m high stand upright on a ground. If their bases (roots) are 4 m apart, then the distance between their tops is ______.
Points A and B are on the opposite edges of a pond as shown in figure. To find the distance between the two points, the surveyor makes a right-angled triangle as shown. Find the distance AB.

