Advertisements
Advertisements
Question
PQR is a triangle right angled at P and M is a point on QR such that PM ⊥ QR. Show that PM2 = QM . MR
Solution
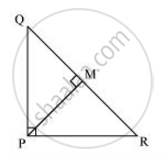
Let ∠MPR = x
In ΔMPR
∠MPR = 180º- 90º - x
∠MRP = 90º - x
Similarity, in ΔMPQ
∠MPQ = 90º - ∠MPR
= 90º - x
∠MQP = 180º - 90º - (90º - x)
∠MQP = x
In ΔQMP and ΔPMR
∠MPQ = ∠MRP
∠PMQ = ∠RMP
∠MQP = ∠MPR
∴ΔQMP ~ ΔPMR (By AAA Similarity criterion)
`=>(QM)/(PM) = (MP)/(MR)`
=>PM2 = QM x MR
APPEARS IN
RELATED QUESTIONS
A ladder leaning against a wall makes an angle of 60° with the horizontal. If the foot of the ladder is 2.5 m away from the wall, find the length of the ladder
If ABC is an equilateral triangle of side a, prove that its altitude = ` \frac { \sqrt { 3 } }{ 2 } a`
ABC is an equilateral triangle of side 2a. Find each of its altitudes.
A tree is broken at a height of 5 m from the ground and its top touches the ground at a distance of 12 m from the base of the tree. Find the original height of the tree.
In ∆PQR, point S is the midpoint of side QR. If PQ = 11, PR = 17, PS = 13, find QR.
A ladder 13 m long rests against a vertical wall. If the foot of the ladder is 5 m from the foot of the wall, find the distance of the other end of the ladder from the ground.
Find the value of (sin2 33 + sin2 57°)
In triangle PQR, angle Q = 90°, find: PR, if PQ = 8 cm and QR = 6 cm
If in a ΔPQR, PR2 = PQ2 + QR2, then the right angle of ∆PQR is at the vertex ________
For going to a city B from city A, there is a route via city C such that AC ⊥ CB, AC = 2x km and CB = 2(x + 7) km. It is proposed to construct a 26 km highway which directly connects the two cities A and B. Find how much distance will be saved in reaching city B from city A after the construction of the highway.
