Advertisements
Advertisements
Question
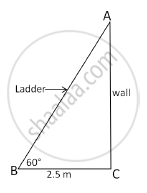
A ladder leaning against a wall makes an angle of 60° with the horizontal. If the foot of the ladder is 2.5 m away from the wall, find the length of the ladder
Solution
Let AB be the ladder and CA be the wall.
The ladder makes an angle of 60° with the horizontal.
∴ΔABC is a 30°-60°-90°, right triangle.
Given: BC = 2.5 m, ∠ABC = 60°
∴AB = 5 cm and ∠BAC = 30°
From Pythagoras Theorem, we have
AB2 = BC2 + CA2
∴52 = (2.5)2 + (CA)2
∴(CA)2 = 25 – 6.25 = 18.75 m
Hence, length of the ladder is `sqrt18.75~~4.33m`
APPEARS IN
RELATED QUESTIONS
The diagonal of a rectangular field is 16 metres more than the shorter side. If the longer side is 14 metres more than the shorter side, then find the lengths of the sides of the field.
ABC is a right triangle right-angled at C. Let BC = a, CA = b, AB = c and let p be the length of perpendicular from C on AB, prove that
(i) cp = ab
`(ii) 1/p^2=1/a^2+1/b^2`
Sides of triangle are given below. Determine it is a right triangle or not? In case of a right triangle, write the length of its hypotenuse. 50 cm, 80 cm, 100 cm
Two poles of heights 6 m and 11 m stand on a plane ground. If the distance between the feet of the poles is 12 m, find the distance between their tops.
A man goes 40 m due north and then 50 m due west. Find his distance from the starting point.
M andN are the mid-points of the sides QR and PQ respectively of a PQR, right-angled at Q.
Prove that:
(i) PM2 + RN2 = 5 MN2
(ii) 4 PM2 = 4 PQ2 + QR2
(iii) 4 RN2 = PQ2 + 4 QR2(iv) 4 (PM2 + RN2) = 5 PR2
Determine whether the triangle whose lengths of sides are 3 cm, 4 cm, 5 cm is a right-angled triangle.
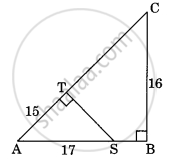
In the given figure, ∠T and ∠B are right angles. If the length of AT, BC and AS (in centimeters) are 15, 16, and 17 respectively, then the length of TC (in centimeters) is ______.
A right-angled triangle may have all sides equal.
Height of a pole is 8 m. Find the length of rope tied with its top from a point on the ground at a distance of 6 m from its bottom.
