Advertisements
Advertisements
Question
M andN are the mid-points of the sides QR and PQ respectively of a PQR, right-angled at Q.
Prove that:
(i) PM2 + RN2 = 5 MN2
(ii) 4 PM2 = 4 PQ2 + QR2
(iii) 4 RN2 = PQ2 + 4 QR2(iv) 4 (PM2 + RN2) = 5 PR2
Solution
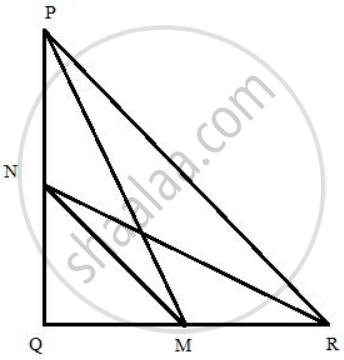
We draw, PM, MN, NR
Pythagoras theorem states that in a right-angled triangle, the square on the hypotenuse is equal to the sum of the squares on the remaining two sides.
Since M and N are the mid-points of the sides QR and PQ respectively, therefore, PN = NQ, QM = RM
(i) First, we consider the ΔPQM, and applying Pythagoras theorem we get,
PM2 = PQ2 + MQ2
= ( PN + NQ )2 + MQ2
= PN + NQ2 + 2PN . NQ + MQ2
= MN2+ PN2 + 2PN.NQ ...[From, ΔMNQ, MN2 = NQ2 + MQ2] ......(i)
Now, we consider the ΔRNQ, and applying Pythagoras theorem we get,
RN2 = NQ2 + RQ2
= NQ2 + ( QM + RM )2
= NQ2 + QM2 + RM2 + 2QM .RM
= MN2 + RM2 + 2QM . RM .......(ii)
Adding (i) and (ii) we get,
PM2 + RN2 = MN2 + PN2 + 2PN.NQ + MN2 + RM2 + 2QM. RM
PM2 + RN2 = 2MN2 + PN2 + RM2 + 2PN.NQ + 2QM.RM
PM2 + RN2 = 2MN2 + NQ2 + QM2 + 2(QN2 ) + 2(QM2 )
PM2 + RN2 = 2MN2 + MN2 + 2MN2
PM2 + RN2 = 5MN2
Hence Proved.
(ii) We consider the ΔPQM, and applying Pythagoras theorem we get,
PM2 = PQ2 + MQ2
4PM2 = 4PQ2 + 4MQ2 ...[ Multiply both sides by 4]
4PM2 = 4PQ2 + 4.`(1/2 "QR")^2` ...[ MQ = `1/2` QR ]
4PM2 = 4PQ2 + 4PQ + 4 . `1/4` QR2
4PM2 = 4PQ2 + QR2
Hence Proved.
(iii) We consider the ΔRQN, and applying Pythagoras theorem we get,
RN2 = NQ2 + RQ2
4RN2 = 4NQ2 + 4QR2 ...[ Multiplying both sides by 4]
4RN2 = 4QR2 + 4 .(1/2 PQ)2 ...[ NQ = `1/2` PQ ]
4RN2 = 4QR2 + 4 .`1/4` PQ2
4RN2 = PQ2 + 4QR2
Hence Proved.
(iv) First, we consider the ΔPQM, and applying Pythagoras theorem we get,
PM2 = PQ2 + MQ2
= ( PN + NQ )2 + MQ2
= PN2 + NQ2 + 2PN.NQ + MQ2
= MN2 + PN2 + 2PN.NQ ...[ From, ΔMNQ, = MN2 = NQ2 + MQ2 ] ......(i)
Now, we consider the ΔRNQ, and applying Pythagoras theorem we get,
RN2 + NQ2 + RQ2
= NQ2 + ( QM + RM )2
= NQ2 + QM2 + RM2 + 2QM .RM
= MN2 + RM2 + 2QM . RM .......(ii)
Adding (i) and (ii) we get,
PM2 + RN2 = MN2 + PN2 + 2PN . NQ + MN2 + RM2 + 2QM. RM
PM2 + RN2 = 2MN2 + PN2 + RM2 + 2PN . NQ + 2QM . RM
PM2 + RN2 = 2MN2 + NQ2 + QM2 + 2(QN2 ) + 2(QM2 )
PM2 + RN2 = 2MN2 + MN2 + 2MN2
PM 2 + RN2 = 5MN2
4( PM2 + RN2 ) = 4.5. (NQ2 + MQ2)
4( PM2 + RN2 ) = 4.5. `[ ( 1/2 "PQ" )^2 + ( 1/2 "RQ" )^2 ] ....[ ∵ "NQ" = 1/2 "PQ" , "MQ" = 1/2 "QR" ]`
4 ( PM2 + RN2 ) = 5PR2
Hence Proved.
APPEARS IN
RELATED QUESTIONS
ABC is an isosceles triangle right angled at C. Prove that AB2 = 2AC2
Prove that the sum of the squares of the sides of a rhombus is equal to the sum of the squares of its diagonals
In the given figure, ∠DFE = 90°, FG ⊥ ED, If GD = 8, FG = 12, find (1) EG (2) FD and (3) EF

Walls of two buildings on either side of a street are parallel to each other. A ladder 5.8 m long is placed on the street such that its top just reaches the window of a building at the height of 4 m. On turning the ladder over to the other side of the street, its top touches the window of the other building at a height 4.2 m. Find the width of the street.
A ladder 13 m long rests against a vertical wall. If the foot of the ladder is 5 m from the foot of the wall, find the distance of the other end of the ladder from the ground.
The given figure shows a quadrilateral ABCD in which AD = 13 cm, DC = 12 cm, BC = 3 cm and ∠ABD = ∠BCD = 90o. Calculate the length of AB.
In figure AB = BC and AD is perpendicular to CD.
Prove that: AC2 = 2BC. DC.
If P and Q are the points on side CA and CB respectively of ΔABC, right angled at C, prove that (AQ2 + BP2) = (AB2 + PQ2)
Use the information given in the figure to find the length AD.

In the figure below, find the value of 'x'.

The sides of the triangle are given below. Find out which one is the right-angled triangle?
11, 60, 61
A right triangle has hypotenuse p cm and one side q cm. If p - q = 1, find the length of third side of the triangle.
A point OI in the interior of a rectangle ABCD is joined with each of the vertices A, B, C and D. Prove that OB2 + OD2 = OC2 + OA2
In a right-angled triangle PQR, right-angled at Q, S and T are points on PQ and QR respectively such as PT = SR = 13 cm, QT = 5 cm and PS = TR. Find the length of PQ and PS.
If ΔABC ~ ΔPQR, `("ar" triangle "ABC")/("ar" triangle "PQR") = 9/4` and AB = 18 cm, then the length of PQ is ______.
Foot of a 10 m long ladder leaning against a vertical wall is 6 m away from the base of the wall. Find the height of the point on the wall where the top of the ladder reaches.
A flag pole 18 m high casts a shadow 9.6 m long. Find the distance of the top of the pole from the far end of the shadow.
In the given figure, AD is a median of a triangle ABC and AM ⊥ BC. Prove that:

(i) `"AC"^2 = "AD"^2 + "BC"."DM" + (("BC")/2)^2`
(ii) `"AB"^2 = "AD"^2 - "BC"."DM" + (("BC")/2)^2`
(iii) `"AC"^2 + "AB"^2 = 2"AD"^2 + 1/2"BC"^2`
Height of a pole is 8 m. Find the length of rope tied with its top from a point on the ground at a distance of 6 m from its bottom.
