Advertisements
Advertisements
Question
In the figure below, find the value of 'x'.

Solution
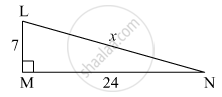
In the right-angled triangle LMN,
∠M = 90°
∴ Side LN is the hypotenuse.
According to Pythagoras' theorem,
l(LN)2 = l(LM)2 + l(MN)2
⇒ (x)2 = (7)2 + (24)2
⇒ x2 = 49 + 576
⇒ x2 = 625
⇒ x = `root 625`
⇒ x = 25
∴ The value of x is 25.
RELATED QUESTIONS
A ladder leaning against a wall makes an angle of 60° with the horizontal. If the foot of the ladder is 2.5 m away from the wall, find the length of the ladder
A man goes 10 m due east and then 24 m due north. Find the distance from the starting point
A ladder 10 m long reaches a window 8 m above the ground. Find the distance of the foot of the ladder from base of the wall.
If the angles of a triangle are 30°, 60°, and 90°, then shown that the side opposite to 30° is half of the hypotenuse, and the side opposite to 60° is `sqrt(3)/2` times of the hypotenuse.
In the given figure, angle ACB = 90° = angle ACD. If AB = 10 m, BC = 6 cm and AD = 17 cm, find :
(i) AC
(ii) CD

The sides of the triangle are given below. Find out which one is the right-angled triangle?
11, 60, 61
A ladder 25m long reaches a window of a building 20m above the ground. Determine the distance of the foot of the ladder from the building.
Determine whether the triangle whose lengths of sides are 3 cm, 4 cm, 5 cm is a right-angled triangle.
Choose the correct alternative:
If length of sides of a triangle are a, b, c and a2 + b2 = c2, then which type of triangle it is?
If the areas of two circles are the same, they are congruent.
