Advertisements
Advertisements
प्रश्न
In the figure below, find the value of 'x'.

उत्तर
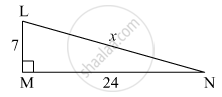
In the right-angled triangle LMN,
∠M = 90°
∴ Side LN is the hypotenuse.
According to Pythagoras' theorem,
l(LN)2 = l(LM)2 + l(MN)2
⇒ (x)2 = (7)2 + (24)2
⇒ x2 = 49 + 576
⇒ x2 = 625
⇒ x = `root 625`
⇒ x = 25
∴ The value of x is 25.
संबंधित प्रश्न
In Fig., ∆ABC is an obtuse triangle, obtuse angled at B. If AD ⊥ CB, prove that AC2 = AB2 + BC2 + 2BC × BD
In an equilateral triangle, prove that three times the square of one side is equal to four times the square of one of its altitudes.
In the given figure, ABC is a triangle in which ∠ABC> 90° and AD ⊥ CB produced. Prove that AC2 = AB2 + BC2 + 2BC.BD.

Find the perimeter of the rectangle whose length is 40 cm and a diagonal is 41 cm.
In figure AB = BC and AD is perpendicular to CD.
Prove that: AC2 = 2BC. DC.
A boy first goes 5 m due north and then 12 m due east. Find the distance between the initial and the final position of the boy.
To get from point A to point B you must avoid walking through a pond. You must walk 34 m south and 41 m east. To the nearest meter, how many meters would be saved if it were possible to make a way through the pond?
For going to a city B from city A, there is a route via city C such that AC ⊥ CB, AC = 2x km and CB = 2(x + 7) km. It is proposed to construct a 26 km highway which directly connects the two cities A and B. Find how much distance will be saved in reaching city B from city A after the construction of the highway.
In a right-angled triangle ABC, if angle B = 90°, BC = 3 cm and AC = 5 cm, then the length of side AB is ______.
Two squares are congruent, if they have same ______.
