Advertisements
Advertisements
प्रश्न
A boy first goes 5 m due north and then 12 m due east. Find the distance between the initial and the final position of the boy.
उत्तर
Given: Direction of north = 5 m i.e. AC Direction of east = 12 m i.e. AB
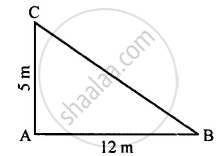
To find: BC
According to Pythagoras Theorem,
In right angled Δ ABC
(BC)2 = (AC)2 + (AB)2
(BC)2 = (5)2 + (12)2
(BC)2 = 25 + 144
(BC)2= 169
∴ BC = `sqrt169=sqrt(13xx13)` = 13 m
APPEARS IN
संबंधित प्रश्न
Prove that the diagonals of a rectangle ABCD, with vertices A(2, -1), B(5, -1), C(5, 6) and D(2, 6), are equal and bisect each other.
A man goes 10 m due east and then 24 m due north. Find the distance from the starting point
ABC is an isosceles triangle right angled at C. Prove that AB2 = 2AC2
In an equilateral triangle, prove that three times the square of one side is equal to four times the square of one of its altitudes.
Nazima is fly fishing in a stream. The tip of her fishing rod is 1.8 m above the surface of the water and the fly at the end of the string rests on the water 3.6 m away and 2.4 m from a point directly under the tip of the rod. Assuming that her string (from the tip of her rod to the fly) is taut, ho much string does she have out (see Figure)? If she pulls in the string at the rate of 5 cm per second, what will be the horizontal distance of the fly from her after 12 seconds?

A tree is broken at a height of 5 m from the ground and its top touches the ground at a distance of 12 m from the base of the tree. Find the original height of the tree.
Digonals of parallelogram WXYZ intersect at point O. If OY =5, find WY.
Prove that (1 + cot A - cosec A ) (1 + tan A + sec A) = 2
In the figure, find AR
If S is a point on side PQ of a ΔPQR such that PS = QS = RS, then ______.
