Advertisements
Advertisements
Question
A boy first goes 5 m due north and then 12 m due east. Find the distance between the initial and the final position of the boy.
Solution
Given: Direction of north = 5 m i.e. AC Direction of east = 12 m i.e. AB
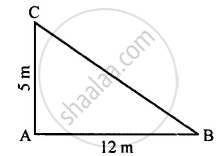
To find: BC
According to Pythagoras Theorem,
In right angled Δ ABC
(BC)2 = (AC)2 + (AB)2
(BC)2 = (5)2 + (12)2
(BC)2 = 25 + 144
(BC)2= 169
∴ BC = `sqrt169=sqrt(13xx13)` = 13 m
APPEARS IN
RELATED QUESTIONS
If ABC is an equilateral triangle of side a, prove that its altitude = ` \frac { \sqrt { 3 } }{ 2 } a`
P and Q are the mid-points of the sides CA and CB respectively of a ∆ABC, right angled at C. Prove that:
`(i) 4AQ^2 = 4AC^2 + BC^2`
`(ii) 4BP^2 = 4BC^2 + AC^2`
`(iii) (4AQ^2 + BP^2 ) = 5AB^2`
In Figure, ABD is a triangle right angled at A and AC ⊥ BD. Show that AB2 = BC × BD

In the figure, given below, AD ⊥ BC.
Prove that: c2 = a2 + b2 - 2ax.
In triangle ABC, angle A = 90o, CA = AB and D is the point on AB produced.
Prove that DC2 - BD2 = 2AB.AD.
A ladder 15m long reaches a window which is 9m above the ground on one side of a street. Keeping its foot at the same point, the ladder is turned to other side of the street to reach a window 12m high. Find the width of the street.
The foot of a ladder is 6m away from a wall and its top reaches a window 8m above the ground. If the ladder is shifted in such a way that its foot is 8m away from the wall to what height does its tip reach?
A flag pole 18 m high casts a shadow 9.6 m long. Find the distance of the top of the pole from the far end of the shadow.
The top of a broken tree touches the ground at a distance of 12 m from its base. If the tree is broken at a height of 5 m from the ground then the actual height of the tree is ______.
Two squares are congruent, if they have same ______.
