Advertisements
Advertisements
Question
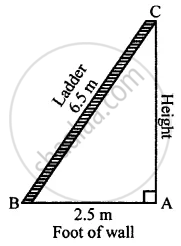
A ladder, 6.5 m long, rests against a vertical wall. If the foot of the ladder is 2.5 m from the foot of the wall, find up to how much height does the ladder reach?
Solution
Given :
Length of ladder = 6.5 m
Length of the foot of the wall = 2.5 m
To find: Height AC According to Pythagoras Theorem,
(BC)2 = (AB)2 + (AC)2
(6.5)2 = (2.5)2 + (AC)2
42.25 = 6.25 + AC2
AC2 = 42.25 – 6.25 = 36 m
AC = `sqrt(6xx6)` = 6 m
∴ Height of wall = 6 m
APPEARS IN
RELATED QUESTIONS
In a right triangle ABC, right-angled at B, BC = 12 cm and AB = 5 cm. The radius of the circle inscribed in the triangle (in cm) is
(A) 4
(B) 3
(C) 2
(D) 1
Identify, with reason, if the following is a Pythagorean triplet.
(24, 70, 74)
In ∆ABC, AB = 10, AC = 7, BC = 9, then find the length of the median drawn from point C to side AB.
In the given figure, AB//CD, AB = 7 cm, BD = 25 cm and CD = 17 cm;
find the length of side BC.
The given figure shows a quadrilateral ABCD in which AD = 13 cm, DC = 12 cm, BC = 3 cm and ∠ABD = ∠BCD = 90o. Calculate the length of AB.
In a right angled triangle, the hypotenuse is the greatest side
Find the unknown side in the following triangles
In the adjoining figure, a tangent is drawn to a circle of radius 4 cm and centre C, at the point S. Find the length of the tangent ST, if CT = 10 cm.

The top of a broken tree touches the ground at a distance of 12 m from its base. If the tree is broken at a height of 5 m from the ground then the actual height of the tree is ______.
Points A and B are on the opposite edges of a pond as shown in figure. To find the distance between the two points, the surveyor makes a right-angled triangle as shown. Find the distance AB.

