Advertisements
Advertisements
Question
In the adjoining figure, a tangent is drawn to a circle of radius 4 cm and centre C, at the point S. Find the length of the tangent ST, if CT = 10 cm.

Options
`sqrt(21)` cm
`3sqrt(21)` cm
`2sqrt(21)` cm
`4sqrt(21)` cm
Solution
`2sqrt(21)` cm
Explanation:
The line from the centre to the tangent is perpendicular to the tangent.
∴ CS ⊥ ST
So, in right angled ΔCST, by the Pythagoras theorem,
CT2 = CS2 + ST2
(10)2 = (4)2 + ST2
ST2 = 100 – 16 = 84
⇒ ST = `2sqrt(21)`
Thus, the length of ST is `2sqrt(21)` cm.
APPEARS IN
RELATED QUESTIONS
In triangle ABC, ∠C=90°. Let BC= a, CA= b, AB= c and let 'p' be the length of the perpendicular from 'C' on AB, prove that:
1. cp = ab
2. `1/p^2=1/a^2+1/b^2`
In Fig., ∆ABC is an obtuse triangle, obtuse angled at B. If AD ⊥ CB, prove that AC2 = AB2 + BC2 + 2BC × BD
An aeroplane leaves an airport and flies due north at a speed of 1,000 km per hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1,200 km per hour. How far apart will be the two planes after `1 1/2` hours?
D and E are points on the sides CA and CB respectively of a triangle ABC right angled at C. Prove that AE2 + BD2 = AB2 + DE2
The diagonals of a rhombus measure 16 cm and 30 cm. Find its perimeter.
In the given figure, AB//CD, AB = 7 cm, BD = 25 cm and CD = 17 cm;
find the length of side BC.
Two poles of heights 6 m and 11 m stand vertically on a plane ground. If the distance between their feet is 12 m;
find the distance between their tips.
In triangle ABC, angle A = 90o, CA = AB and D is the point on AB produced.
Prove that DC2 - BD2 = 2AB.AD.
Diagonals of rhombus ABCD intersect each other at point O.
Prove that: OA2 + OC2 = 2AD2 - `"BD"^2/2`
In a quadrilateral ABCD, ∠B = 90° and ∠D = 90°.
Prove that: 2AC2 - AB2 = BC2 + CD2 + DA2
Triangle XYZ is right-angled at vertex Z. Calculate the length of YZ, if XY = 13 cm and XZ = 12 cm.
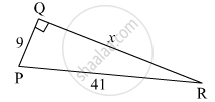
In the figure below, find the value of 'x'.
Find the Pythagorean triplet from among the following set of numbers.
4, 7, 8
The sides of the triangle are given below. Find out which one is the right-angled triangle?
8, 15, 17
Find the unknown side in the following triangles
In a quadrilateral ABCD, ∠A + ∠D = 90°. Prove that AC2 + BD2 = AD2 + BC2
[Hint: Produce AB and DC to meet at E.]
In the given figure, AD is a median of a triangle ABC and AM ⊥ BC. Prove that:

(i) `"AC"^2 = "AD"^2 + "BC"."DM" + (("BC")/2)^2`
(ii) `"AB"^2 = "AD"^2 - "BC"."DM" + (("BC")/2)^2`
(iii) `"AC"^2 + "AB"^2 = 2"AD"^2 + 1/2"BC"^2`
The top of a broken tree touches the ground at a distance of 12 m from its base. If the tree is broken at a height of 5 m from the ground then the actual height of the tree is ______.
Two trees 7 m and 4 m high stand upright on a ground. If their bases (roots) are 4 m apart, then the distance between their tops is ______.
If the hypotenuse of one right triangle is equal to the hypotenuse of another right triangle, then the triangles are congruent.
