Advertisements
Advertisements
Question
In triangle ABC, ∠C=90°. Let BC= a, CA= b, AB= c and let 'p' be the length of the perpendicular from 'C' on AB, prove that:
1. cp = ab
2. `1/p^2=1/a^2+1/b^2`
Solution
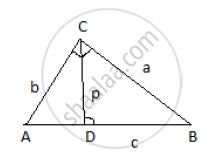
1. Area of a triangle = (1/2) x Base x Height
A(ΔABC) = (1/2) x AB x CD
A(ΔABC) = (1/2) x cp .......(i)
Area of right angle triangle ABC = A(ΔABC) = (1/2) x AC x BC
A(ΔABC) = (1/2) x ba ........(ii)
From (i) and (ii)
cp=ba⇒ cp⇒ab ..........(iii)
2. We have,
cp=ab ..........From(iii)
p = ab/c
Square both sides of the equation.
We get, `p^2=(a^2b^2)/c^2`
`1/p^2=c^2/(a^2b^2)" ..................(iv).....[By invertendo]"`
In right angled triangle ABC,
AB2 = AC2 + BC2 ................[By Pythagoras’ theorem]
c2 = b2 + a2 ............(v)
`c^2/(a^2b^2) = b^2/(a^2b^2) + a^2/(a^2b^2)`..........[Dividing throughout by `a^2b^2`]
`c^2/(ab)^2 = 1/a^2 + 1/b^2` .........(iii)
`c^2/(cp)^2 = 1/a^2 + 1/b^2` ...........[From (ii) and (iii)]
`c^2/(c^2p^2) = 1/a^2 + 1/b^2`
`1/p^2 = 1/a^2 + 1/b^2`
APPEARS IN
RELATED QUESTIONS
In Fig., ∆ABC is an obtuse triangle, obtuse angled at B. If AD ⊥ CB, prove that AC2 = AB2 + BC2 + 2BC × BD
ABCD is a rhombus. Prove that AB2 + BC2 + CD2 + DA2= AC2 + BD2
Nazima is fly fishing in a stream. The tip of her fishing rod is 1.8 m above the surface of the water and the fly at the end of the string rests on the water 3.6 m away and 2.4 m from a point directly under the tip of the rod. Assuming that her string (from the tip of her rod to the fly) is taut, ho much string does she have out (see Figure)? If she pulls in the string at the rate of 5 cm per second, what will be the horizontal distance of the fly from her after 12 seconds?

The diagonals of a rhombus measure 16 cm and 30 cm. Find its perimeter.
In the given figure, ∆ABC is an equilateral triangle of side 3 units. Find the coordinates of the other two vertices ?

Find the side and perimeter of a square whose diagonal is 10 cm.
Some question and their alternative answer are given. Select the correct alternative.
If a, b, and c are sides of a triangle and a2 + b2 = c2, name the type of triangle.
Pranali and Prasad started walking to the East and to the North respectively, from the same point and at the same speed. After 2 hours distance between them was \[15\sqrt{2}\]
km. Find their speed per hour.
A man goes 40 m due north and then 50 m due west. Find his distance from the starting point.
Find the value of (sin2 33 + sin2 57°)
The sides of a certain triangle is given below. Find, which of them is right-triangle
16 cm, 20 cm, and 12 cm
The length of the diagonals of rhombus are 24cm and 10cm. Find each side of the rhombus.
In a triangle ABC right angled at C, P and Q are points of sides CA and CB respectively, which divide these sides the ratio 2 : 1.
Prove that: 9AQ2 = 9AC2 + 4BC2
There are two paths that one can choose to go from Sarah’s house to James's house. One way is to take C street, and the other way requires to take B street and then A street. How much shorter is the direct path along C street?

An isosceles triangle has equal sides each 13 cm and a base 24 cm in length. Find its height
In ΔABC, if DE || BC, AD = x, DB = x – 2, AE = x + 2 and EC = x – 1, then value of x is ______.
A flag pole 18 m high casts a shadow 9.6 m long. Find the distance of the top of the pole from the far end of the shadow.
Two rectangles are congruent, if they have same ______ and ______.
A right-angled triangle may have all sides equal.
