Advertisements
Advertisements
प्रश्न
In triangle ABC, ∠C=90°. Let BC= a, CA= b, AB= c and let 'p' be the length of the perpendicular from 'C' on AB, prove that:
1. cp = ab
2. `1/p^2=1/a^2+1/b^2`
उत्तर
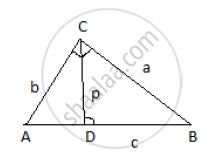
1. Area of a triangle = (1/2) x Base x Height
A(ΔABC) = (1/2) x AB x CD
A(ΔABC) = (1/2) x cp .......(i)
Area of right angle triangle ABC = A(ΔABC) = (1/2) x AC x BC
A(ΔABC) = (1/2) x ba ........(ii)
From (i) and (ii)
cp=ba⇒ cp⇒ab ..........(iii)
2. We have,
cp=ab ..........From(iii)
p = ab/c
Square both sides of the equation.
We get, `p^2=(a^2b^2)/c^2`
`1/p^2=c^2/(a^2b^2)" ..................(iv).....[By invertendo]"`
In right angled triangle ABC,
AB2 = AC2 + BC2 ................[By Pythagoras’ theorem]
c2 = b2 + a2 ............(v)
`c^2/(a^2b^2) = b^2/(a^2b^2) + a^2/(a^2b^2)`..........[Dividing throughout by `a^2b^2`]
`c^2/(ab)^2 = 1/a^2 + 1/b^2` .........(iii)
`c^2/(cp)^2 = 1/a^2 + 1/b^2` ...........[From (ii) and (iii)]
`c^2/(c^2p^2) = 1/a^2 + 1/b^2`
`1/p^2 = 1/a^2 + 1/b^2`
APPEARS IN
संबंधित प्रश्न
The points A(4, 7), B(p, 3) and C(7, 3) are the vertices of a right traingle ,right-angled at B. Find the values of p.
PQR is a triangle right angled at P. If PQ = 10 cm and PR = 24 cm, find QR.
Prove that the points A(0, −1), B(−2, 3), C(6, 7) and D(8, 3) are the vertices of a rectangle ABCD?
In the given figure, point T is in the interior of rectangle PQRS, Prove that, TS2 + TQ2 = TP2 + TR2 (As shown in the figure, draw seg AB || side SR and A-T-B)

In ∆ABC, ∠BAC = 90°, seg BL and seg CM are medians of ∆ABC. Then prove that:
4(BL2 + CM2) = 5 BC2

Digonals of parallelogram WXYZ intersect at point O. If OY =5, find WY.

In ΔMNP, ∠MNP = 90˚, seg NQ ⊥ seg MP, MQ = 9, QP = 4, find NQ.
Find the length of diagonal of the square whose side is 8 cm.
Find the value of (sin2 33 + sin2 57°)
Find the Pythagorean triplet from among the following set of numbers.
3, 4, 5
A right triangle has hypotenuse p cm and one side q cm. If p - q = 1, find the length of third side of the triangle.
The length of the diagonals of rhombus are 24cm and 10cm. Find each side of the rhombus.
In a triangle ABC right angled at C, P and Q are points of sides CA and CB respectively, which divide these sides the ratio 2 : 1.
Prove that : 9(AQ2 + BP2) = 13AB2
There are two paths that one can choose to go from Sarah’s house to James's house. One way is to take C street, and the other way requires to take B street and then A street. How much shorter is the direct path along C street?

Find the unknown side in the following triangles
An isosceles triangle has equal sides each 13 cm and a base 24 cm in length. Find its height
In figure, PQR is a right triangle right angled at Q and QS ⊥ PR. If PQ = 6 cm and PS = 4 cm, find QS, RS and QR.
Two trees 7 m and 4 m high stand upright on a ground. If their bases (roots) are 4 m apart, then the distance between their tops is ______.
Jiya walks 6 km due east and then 8 km due north. How far is she from her starting place?
Jayanti takes shortest route to her home by walking diagonally across a rectangular park. The park measures 60 metres × 80 metres. How much shorter is the route across the park than the route around its edges?
